Упражнение 1.26
Покажите, что если 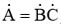 , то и A = BC, где A, B и C - модули комплексных чисел. Подсказка: представьте каждое из комплексных чисел в полярной форме, например,
, то и A = BC, где A, B и C - модули комплексных чисел. Подсказка: представьте каждое из комплексных чисел в полярной форме, например, 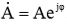 .
.
В наличии: 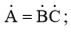 (1)
(1) 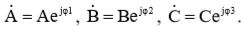 (2)
(2)
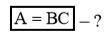
Вычисления будут производиться с помощью комплексных величин, как и описано в книге. Поэтому, для полного понимания предмета, следует предварительно прочесть Приложение А книги по теме комплексных чисел.
Для того, чтобы найти решение упражнения, нужно просто выражение (2) подставить в формулу (1):
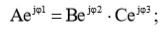
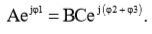 (3)
(3)
Из выражения (3) очевидно, что: 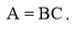
Упражнение 1.27 (необязательное)
Докажите, что в электрической цепи, где протекающий ток сдвинут по фазе на 90° относительно напряжения, в среднем за период мощность не потребляется.
В наличии: 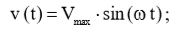 (1)
(1) 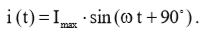 (2)
(2)
Pmid(Δt = T) – ?
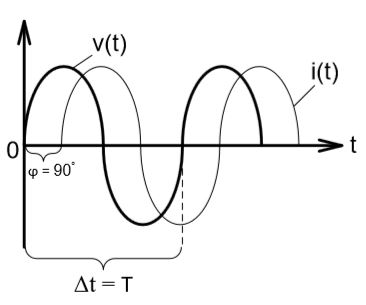
Итак, у нас в наличии две синусоидальные функции напряжения v(t) и тока i(t), изменяющиеся во времени t, с амплитудами Vmax и Imax, сдвинутых друг относительно друга на 90°, где ω – угловая частота сигнала.
Выражение (2) можно переписать в виде косинуса: 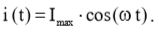 (3)
(3)
Средняя мощность за промежуток времени Δt по определению является отношением полной мощности P(Δt), потребленной за время Δt, к величине Δt: 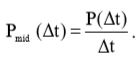 (4)
(4)
Полная мощность за промежуток времени Δt является интегралом от мгновенного значения мощности p(t): 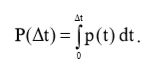 (5)
(5)
Мгновенное значение мощности определяется произведением функций напряжения и тока: 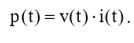 (6)
(6)
C учетом (6), выражение (5) примет вид: 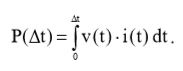 (7)
(7)
Подставив в (7), выражения (1) и (3) мы получаем следующее: 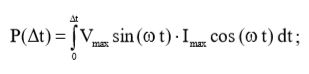
 (8)
(8)
Воспользуемся тригонометрической формулой для произведения синуса и косинуса углов α и β, которая приводится в книге, в Приложении А: 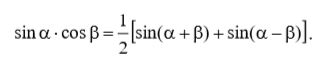 (9)
(9)
Применив формулу (9) к выражению (8), получим: 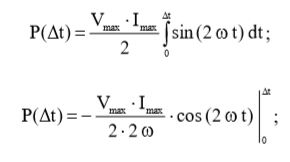
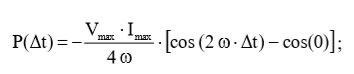
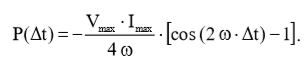 (10)
(10)
С учетом (10), выражение (4) примет вид: 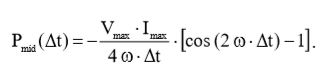 (11)
(11)
Угловая частота ω определяется следующим общеизвестным уравнением: 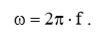 (12)
(12)
Частота сигнала f обратно пропорциональна его периоду T: 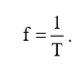 (13)
(13)
С учетом (13), выражение для угловой частоты (12) примет вид: 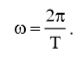 (14)
(14)
С учетом (14), выражение (11) примет окончательный вид: 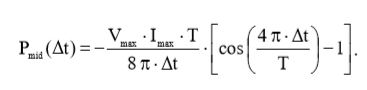 (15)
(15)
Произведем вычисления по формуле (15), для промежутка времени Δt, равного периоду сигнала: 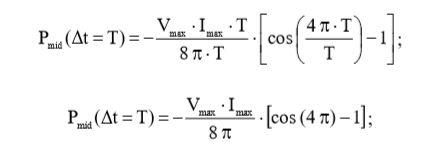
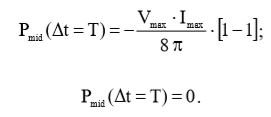
Таким образом, мы доказали, что при условиях, указанных в упражнении, в среднем за период сигнала мощность не потребляется.
Упражнение 1.28
Покажите, что вся средняя мощность, сообщенная предыдущей схеме, потребляется резистором. Для этого подсчитайте величину выражения 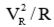 . Какова эта мощность, в ваттах, для последовательной цепи из конденсатора с номиналом 1 мкФ и резистора с номиналом 1 кОм, подключенной к промышленной сети переменного тока с напряжением 115 В и частотой 60 Гц.
. Какова эта мощность, в ваттах, для последовательной цепи из конденсатора с номиналом 1 мкФ и резистора с номиналом 1 кОм, подключенной к промышленной сети переменного тока с напряжением 115 В и частотой 60 Гц.
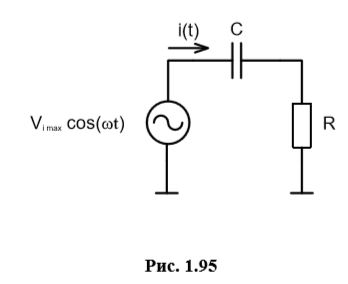
В наличии: Vi = 115 В; f = 60 Гц; R = 1 кОм; C = 1 мкФ.
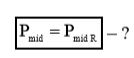
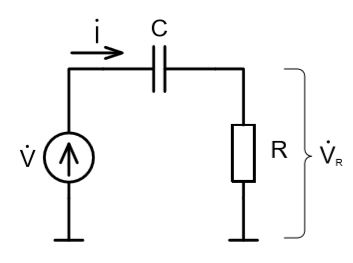
Вычисления будут производиться с помощью комплексных величин, как и описано в книге. Поэтому, для полного понимания предмета, следует предварительно прочесть Приложение А книги по теме комплексных чисел.
Средняя мощность, потребляемая схемой, будет определяться произведением тока и напряжения:
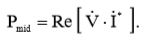 (1)
(1)
Звездочкой помечаются комплексно-сопряженные величины. Средняя потребляемая мощность – величина всегда положительная, поэтому для анализа цепей переменного тока идут на некоторые ухищрения. В формулы вводят комплексно-сопряженные величины, в соответствии с формулой из приложения A: 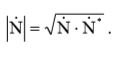 (2)
(2)
Эффективное комплексное напряжение равно:
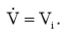 (3)
(3)
В соответствии с законом Ома, ток в схеме можно выразить через входное напряжение 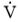 и импеданс схемы Z:
и импеданс схемы Z:  (4)
(4)
Импеданс схемы равен: 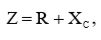 (5)
(5)
где
XC – реактанс конденсатора.
Нам уже известно, что реактанс конденсатора равен: 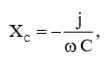 (6)
(6)
где 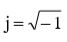 – мнимая единица,
– мнимая единица,
ω – угловая частота сигнала.
С учетом (6), выражение (5) примет следующий вид: 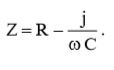 (7)
(7)
Подставив в (4) выражения (3) и (7), получим: 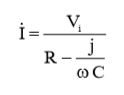
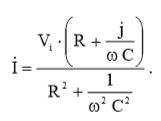 (8)
(8)
В соответствии с выражением (8) определим комплексно-сопряженное число: 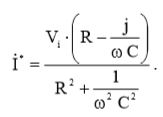 (9)
(9)
Подставив (3) и (9) в (1), получим формулу средней мощности, потребляемой схемой: 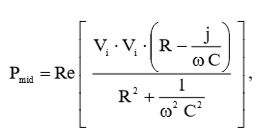
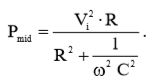 (10)
(10)
В соответствии с условиями упражнения и аналогично формуле мощности в цепи постоянного тока, средняя мощность, потребляемая резистором, будет равна: 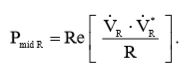 (11)
(11)
Применив к нашей схеме формулу коэффициента передачи по напряжению, выведенную ранее для резистивного делителя, получим: 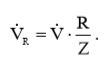 (12)
(12)
С учетом (3) и (7), выражение (12) примет вид: 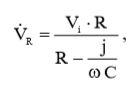
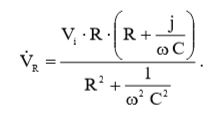 (13)
(13)
В соответствии c (13), комплексно-сопряженное напряжение на резисторе будет равно:
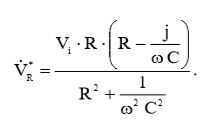 (14)
(14)
Подставим (13) и (14) в (11): 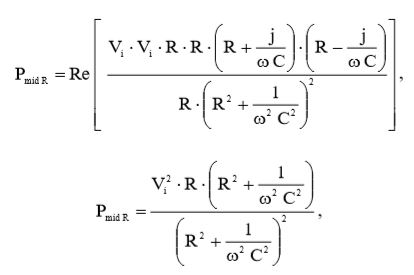
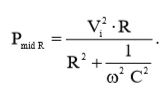 (15)
(15)
Сравнивая выражения (10) и (15), можно прийти к выводу, что они идентичны, следовательно: 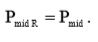
Вычислим среднюю мощность.
В соответствии с выражением (6), величина реактанса конденсатора равна: 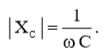 (16)
(16)
Подставив (16) в (15), мы получим: 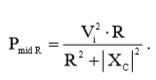 (17)
(17)
Угловая частота связана с частотой сигнала следующим соотношением:
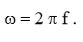 (18)
(18)
Подставив (18) в (16), сможем вычислить величину реактанса конденсатора: 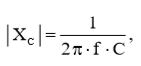
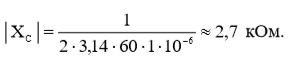 (19)
(19)
Теперь, вычислим по формуле (17), с учетом результатов (19), искомую величину средней мощности: 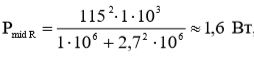
Упражнение 1.29
Покажите, что если последовательно добавить в последовательную RL-цепь конденсатор, с емкостью С = 1/(ω2L), то коэффициент мощности будет равен единице. Затем, то же самое сделайте для параллельного подключения конденсатора к параллельной RL-цепи.
В наличии: R = const.; L = const.; V = const.; ω = const.; 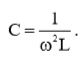 (1)
(1)
а) Последовательное соединение.
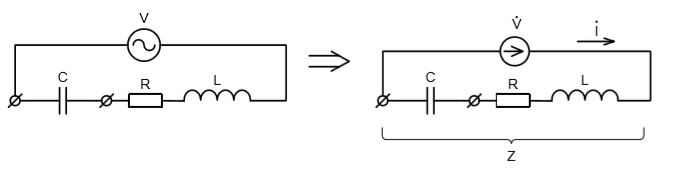
В соответствии с материалами книги, коэффициент мощности равен: 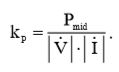 (2)
(2)
Средняя мощность, потребляемая схемой, будет определяться произведением тока и напряжения
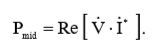 (3)
(3)
Согласно правилам преобразования, эффективное комплексное напряжение в сети равно:  (4)
(4)
По закону Ома, эффективный комплексный ток в схеме равен: 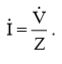 (5)
(5)
Импеданс последовательной схемы равен: 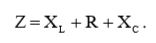 (6)
(6)
Реактанс конденсатора равен: 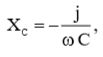 (7)
(7)
где
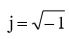 – мнимая единица,
– мнимая единица,
ω – угловая частота сигнала.
Реактанс катушки индуктивности равен: 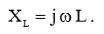 (8)
(8)
Перепишем выражение (6) с учетом (7) и (8): 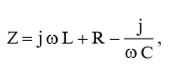
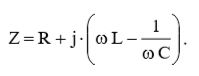 (9)
(9)
Подставив выражения (4) и (9) в (5), получим: 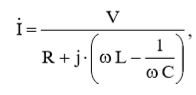
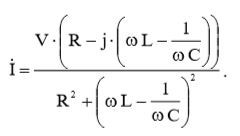 (10)
(10)
В соответствии с выражением (10) определим комплексно-сопряженное число: 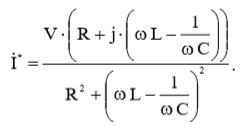 (11)
(11)
Подставив (4) и (11) в (3), получим окончательное выражение для средней потребляемой мощности:
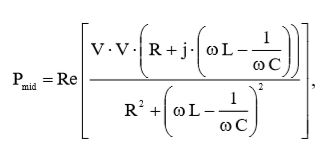
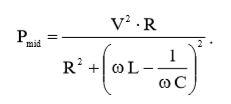 (12)
(12)
С учетом (4), величина эффективного комплексного напряжения равна: 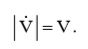 (13)
(13)
С учетом (10), величина эффективного комплексного тока равна: 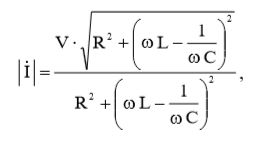
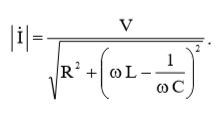 (14)
(14)
Подставив (12), (13) и (14) в (2), мы получим окончательное выражение для коэффициента мощности: 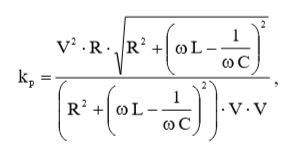
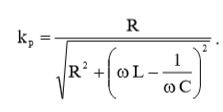 (15)
(15)
Теперь подставим в формулу (15) выражение (1) и вычислим коэффициент мощности:
б) Параллельное соединение.
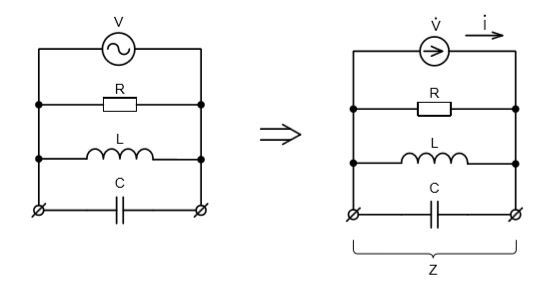
Для параллельного соединения справедливы формулы (2) – (5).
Импеданс параллельной схемы равен: 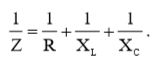 (16)
(16)
Реактансы конденсатора и катушки индуктивности определяются по формулам (7), и (8).
Подставив выражения (7) и (8) в (16), мы получим: 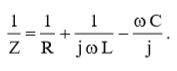 (17)
(17)
С мнимой единицей в знаменателе работать неудобно, поэтому переведем ее в числитель. Для этого умножим и числитель, и знаменатель компонентов формулы (17), где имеется мнимая единица, на мнимую единицу: 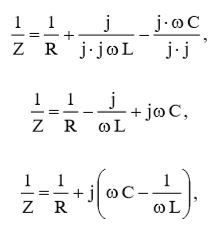
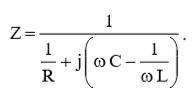 (18)
(18)
Подставив выражения (4) и (18) в (5), получим: 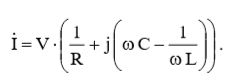 (19)
(19)
В соответствии с выражением (19) определим комплексно-сопряженное число: 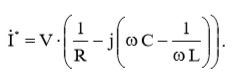 (20)
(20)
Подставив (4) и (20) в (3), получим окончательное выражение для средней потребляемой мощности: 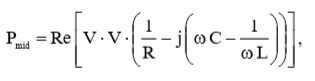
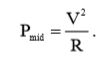 (21)
(21)
Величина эффективного комплексного напряжения будет определяться, как и в предыдущем случае, по формуле (13).
С учетом (19), величина эффективного комплексного тока равна: 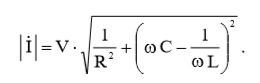 (22)
(22)
Подставив (21), (13) и (22) в (2), мы получим окончательное выражение для коэффициента мощности: 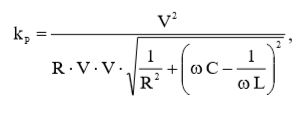
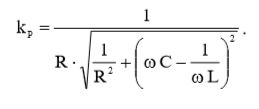 (23)
(23)
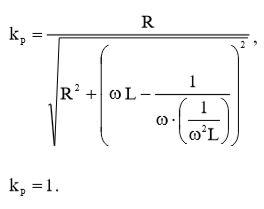
Теперь подставим в формулу (23) выражение (1) и вычислим коэффициент мощности: 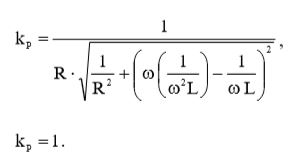
Замечание
Данное упражнение дает представление о механизмах коррекции коэффициента мощности на промышленных предприятиях.
Упражнение 1.30
Покажите, что приведенное ранее выражение для амплитудно-частотной характеристики RC-фильтра низких частот справедливо.

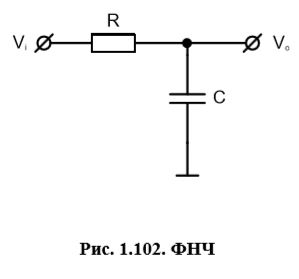
В наличии: R = const.; C = const.; ω = const.
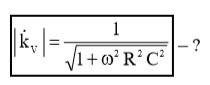
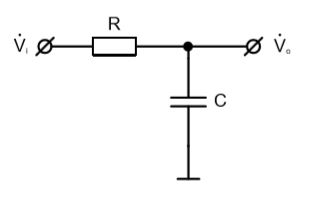
Вычисления будут производиться с помощью комплексных величин, как и описано в книге. Поэтому, для полного понимания предмета, следует предварительно прочесть Приложение А книги по теме комплексных чисел.
Комплексный коэффициент передачи по напряжению равен отношению выходного напряжения к входному напряжению: 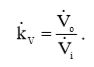 (1)
(1)
Применив к нашей схеме уже знакомую формулу для выходного напряжения простого резистивного делителя, мы получим выражение для выходного напряжения: 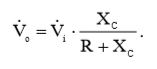 (2)
(2)
Реактанс конденсатора равен: 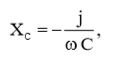 (3)
(3)
где
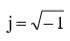 – мнимая единица,
– мнимая единица,
ω – угловая частота сигнала.
Подставив (3) в (2), мы получаем: 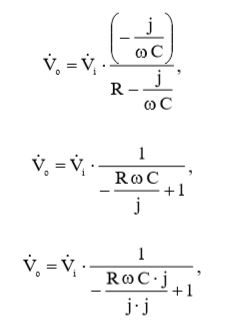
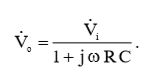 (4)
(4)
Теперь (4) подставляем в (1) и получаем выражение для комплексного коэффициента передачи по напряжению: 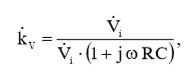
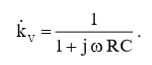 (5)
(5)
В соответствии с выражением (5), величина коэффициента передачи по напряжению будет равна: 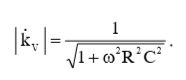











 Опубликована:
Опубликована:


 Вознаградить
Вознаградить



Комментарии (0) |
Я собрал (0) |
Подписаться
|
Я собрал (0) |
Подписаться
Для добавления Вашей сборки необходима регистрация