Упражнения 1.22, 1.23, 1.24, 1.25 "Искусство схемотехники", 3-е издание

Упражнение 1.22 
Спроектируйте симметричный ограничитель, который будет ограничивать сигнал на уровнях -5,6 В и +5,6 В. 
 

В наличии: V_satH = 5,6 В; V_satL = - 5,6 В; V_D = 0,6 В.   
Нарисовать схему. 

Упражнение очень простое, поэтому, прочитав соответствующий раздел книги, можно не задумываясь его выполнить. 

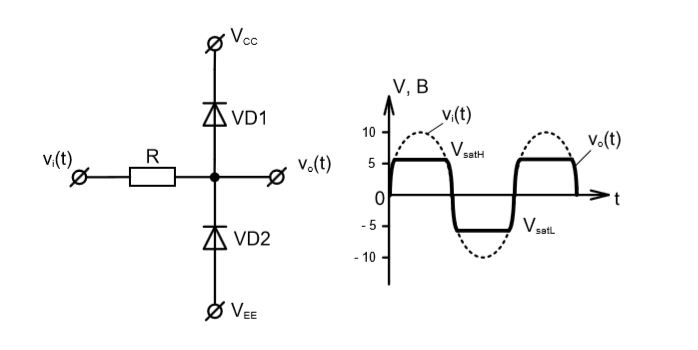
Суть диодных ограничителей состоит в том, чтобы соответствующий диод смещался в прямом направлении, на величину типового падения напряжения на диодах V_D, при уходе входного сигнала v_i(t) за заданные рамки. Таким образом, достигается ограничение входного сигнала в установленных пределах. Резистор R носит функцию токового ограничителя при открытии одного из диодов. 
Теперь определим параметры симметричного источника питания, задающего нужные границы выходного сигнала v_o(t). В этом нам поможет правило Кирхгофа для напряжений.  
Когда диод VD1 открыт, то имеют место следующие соотношения: 

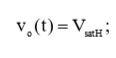
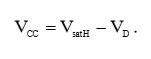(1)

Когда диод VD2 открыт, то имеют место следующие соотношения: 

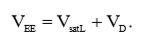(2)

Вычислим по формулам (1) и (2) параметры симметричного источника питания: 

 

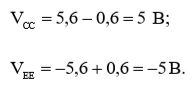
Упражнение 1.23 
Покажите, что предыдущее утверждение верно. 

В книге, тексту упражнения предшествует следующий абзац. 

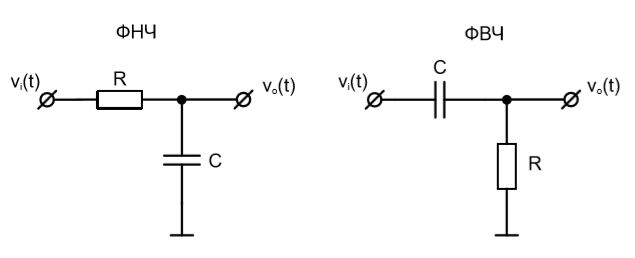
«Все, что нас интересует при проектировании любого из двух простых RC-фильтров (фильтра низких частот или фильтра высоких частот) в составе более сложных устройств, это их входные и выходные импедансы. Задача кажется сложной, поскольку речь идет о четырех импедансах, изменяющихся в зависимости от частоты сигнала. Однако, если вы решите эту задачу верно, то ответ будет простым и одинаковым для всех четырех величин искомых импедансов! 
… 
Итак, ответ поразительно прост: в наихудшем случае все четыре импеданса будут равны R.» 
 
В наличии: R = const., C = const. 

|Z_iMIN| – ?; |Z_oMAX| – ? 

Из материалов книги нам известно, что величина реактанса конденсатора определяется по формуле: 

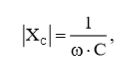(1)

где ω – угловая частота сигнала, Гц. 

Вспомним теорему Тевенина. По отношению к внешней цепи, фильтр низких частот (ФНЧ) и фильтр высоких частот (ФВЧ), являются нагрузкой, представленной последовательно соединенной RC-цепью (вне зависимости от порядка подключения элементов схемы). 

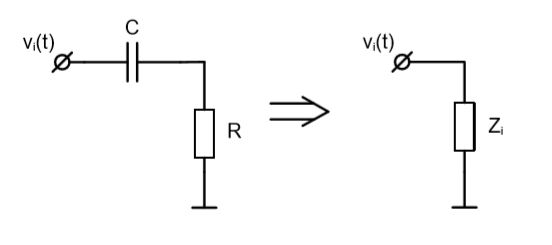
Таким образом, для ФНЧ и ФВЧ, входной импеданс будет равен (без учета фазы сигнала): 

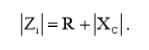(2)

В соответствии с выражением (1), с увеличением частоты реактанс конденсатора будет уменьшаться и в пределе, устремится к нулю. Следовательно, выражение (2) примет вид: 

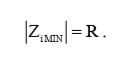
Выходной импеданс для ФНЧ и ФВЧ без учета фазы сигнала будет определяться по формуле выходного сопротивления резистивного делителя: 

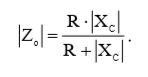(3)

На низких частотах выполняется условие: 

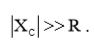(4)

C учетом (4), выражение (3) для выходного импеданса примет окончательный вид: 

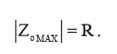
Таким образом, мы доказали справедливость предложенного утверждения и получили практически важный инструмент проектирования фильтров. 

 

Упражнение 1.24 
Спроектируйте двухкаскадный полосовой RC-фильтр, в котором, в качестве первого каскада выступает фильтр высоких частот с частотой среза 100 Гц, а в качестве второго каскада – фильтр низких частот с частотой среза 10 кГц. Источник входного сигнала обладает выходным импедансом в 100 Ом. Чему равен выходной импеданс вашего фильтра в наихудшем случае, и каков при этом минимально рекомендуемый импеданс нагрузки? 
В наличии: f_c1  = 100 Гц; f_c2 = 10 кГц; |Z_S| = 100 Ом. 
R1 – ?; C1 – ?; R2 – ?; C2 – ?; |Z_{o MAX}| – ?; |Z_{L MIN}| – ? 

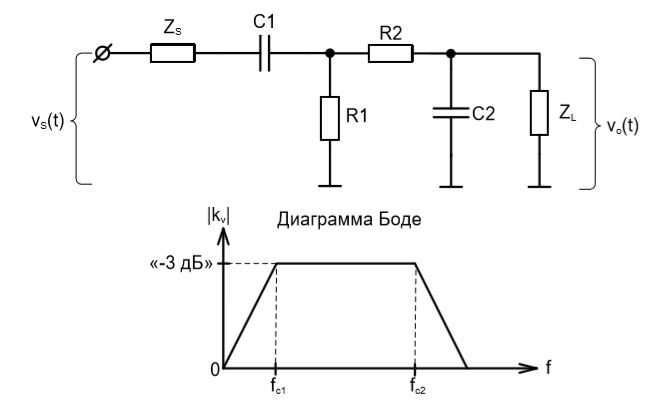
Представим, как первый каскад нагружает источник входного сигнала. 

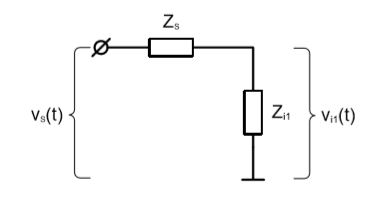
Чтобы первый каскад не оказывал сильного влияния на источник входного сигнала, необходимо, чтобы его входной импеданс Z_i1 был как минимум на порядок больше выходного импеданса источника сигнала Z_s (вспомним резистивный делитель):

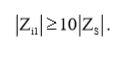(1)

Согласно результатам, полученным из предыдущего упражнения, минимальный входной импеданс первого каскада будет равен: 

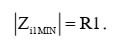(2)

С учетом (2), выражение (1) нам позволит определить величину резистора R1 и рассчитать ее: 

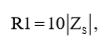(3)

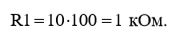(4)

Частота среза первого каскада f_c1, будет определяться по формуле (из пройденного материала книги): 

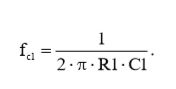(5)

Из выражения (5) выразим, а затем рассчитаем, с учетом результатов вычислений (4), величину емкости конденсатора С1: 

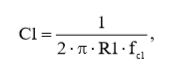
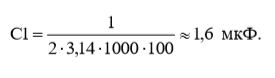
Теперь представим, как второй каскад нагружает первый каскад, в соответствии с теоремой Тевенина. 

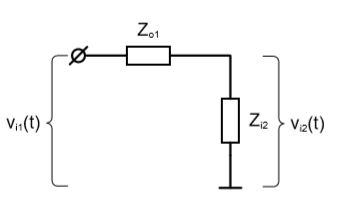
Из предыдущего упражнения нам теперь известно, что максимальный выходной импеданс первого каскада будет равен: 

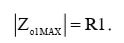(6)

Чтобы второй каскад не оказывал сильного влияния на первый каскад, необходимо, чтобы его входной импеданс Z_i2 был как минимум на порядок больше максимального выходного импеданса первого каскада Z_o1MAX: 

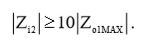(7)

По аналогии с первым каскадом, выражение (2), минимальный входной импеданс второго каскада будет равен: 

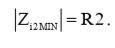(8)

С учетом (4), (6) и (8), выражение (7) нам позволит определить величину резистора R2 и рассчитать ее: 

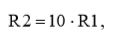(9)

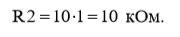(10)

Частота среза первого каскада f_c2, будет равна: 

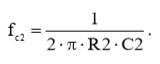(11)

Из выражения (11) выразим, а затем рассчитаем, с учетом результатов вычислений (10), величину емкости конденсатора С2: 

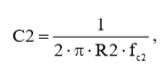(12)

Наконец, представим, как нагрузка Z_L подключена ко второму каскаду, в соответствии с теоремой Тевенина. 

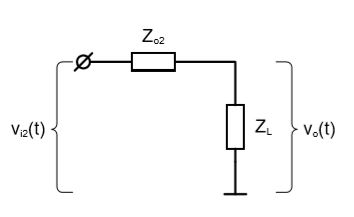
Аналогично первому каскаду (6), максимальный выходной импеданс второго каскада будет равен максимальному выходному импедансу всей схемы: 

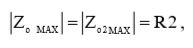(13)

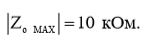(14)

Чтобы нагрузка не оказывала сильного влияния на второй каскад, необходимо, чтобы ее импеданс Z_L был как минимум на порядок больше максимального выходного сопротивления всей схемы Z_{o MAX}: 

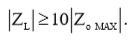(15)

С учетом (14) и (15), минимальный импеданс нагрузки будет равен:

 

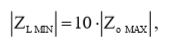
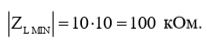
Упражнение 1.25 
Воспользуйтесь приведенными выше выражениями для импеданса при параллельном и последовательном соединении компонентов схем, чтобы  вывести формулы (1.17) и (1.18) для емкости двух конденсаторов а) при параллельном и б) последовательном соединении последних. Подсказка: один конденсатор имеет емкость C1, другой – C2. Запишите выражения для импеданса параллельного и последовательного соединений конденсаторов. Определите из полученных выражений общую емкость С. 
В наличии: 

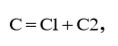(1.17)

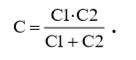(1.18)

 

а) Параллельное соединение. 

 

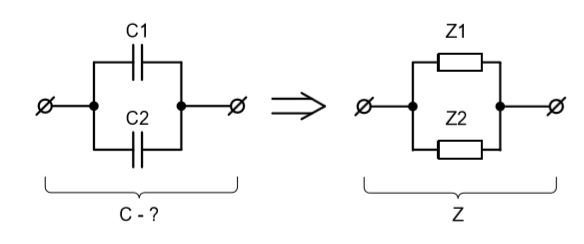
По аналогии с сопротивлением двух параллельно соединенных резисторов, импеданс схемы будет равен: 

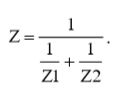(1)

В соответствии с материалами книги и нашей схемой, общий импеданс также равен: 

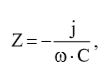(2)

где  
ω – угловая частота, Гц; 

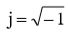 – мнимая единица. 

Выражение (2) можно  видоизменить, умножив и числитель, и знаменатель на мнимую единицу: 

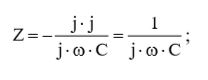
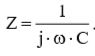(3)

По аналогии с выражением (3), для импедансов Z1 и Z2 мы можем записать следующие выражения: 

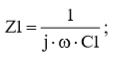(4)

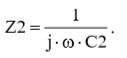(5)

Подставив выражения (3), (4) и (5) в (1), мы сможем определить общую емкость C:

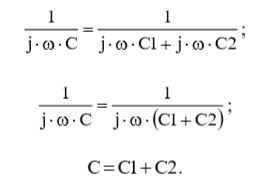
б) Последовательное соединение. 

 

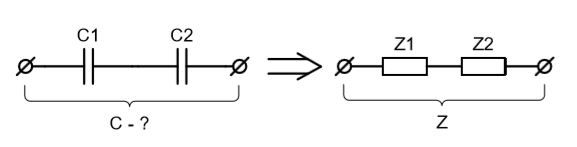
По аналогии с сопротивлением двух последовательно соединенных резисторов, импеданс схемы будет равен: 

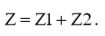(6)

Подставив выражения (3), (4) и (5) в (6), мы сможем определить общую емкость C: