Упражнения 1.3, 1.4, 1.5, 1.6, "Искусство схемотехники", 3-е издание

Упражнение 1.3

Докажите справедливость приведенных выше выражений для двух последовательно и параллельно соединенных резисторов.

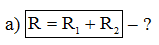
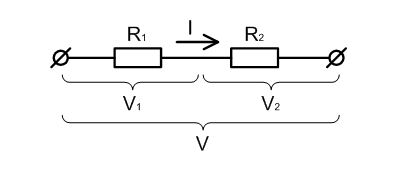
Через каждый из резисторов протекает один и тот же ток.

В соответствии с законом Ома, сопротивление двух последовательно соединенных резисторов равно:

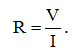(1)

Закон Кирхгофа для напряжений говорит нам, что падение напряжения, на данной цепи, будет равно сумме падений напряжения на каждом из резисторов:

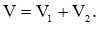(2)

Перепишем выражение (1) с учетом выражения (2):

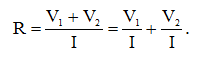(3)

Сопротивления каждого из резисторов также определяются в соответствии с законом Ома:

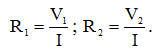(4)

С учетом соотношений (3) и (4) выражение для общего сопротивления двух последовательно соединенных резисторов примет окончательный вид:

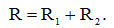
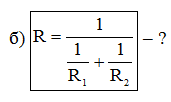
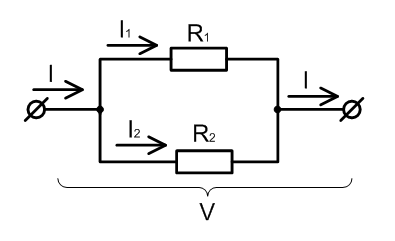
На обоих резисторах, при параллельном соединении, будет одно и то же падение напряжения. Как и в случае последовательного соединения, сопротивление участка цепи, состоящей из двух параллельно соединенных резисторов, будет определяться в соответствии с законом Ома (см. выражение (1)).

Закон Кирхгофа для токов говорит нам, что ток, протекающий через данную цепь, будет равен сумме токов, протекающих через каждый из резисторов:

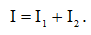(5)

Перепишем выражение (1) с учетом выражения (5):

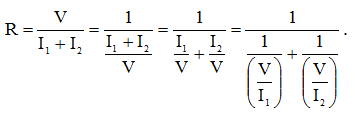(6)

Сопротивления каждого из резисторов определяются в соответствии с законом Ома:

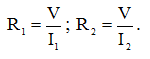(7)

С учетом соотношений (6) и (7) выражение для общего сопротивления двух параллельно соединенных резисторов примет окончательный вид:

 

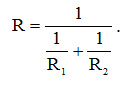
Упражнение 1.4

Покажите, что сопротивление нескольких, параллельно соединенных резисторов будет равно:

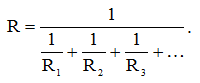
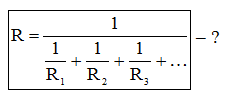
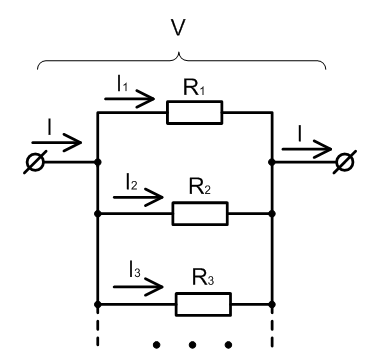
Решаем аналогично предыдущему упражнению (пункт б)).

На всех резисторах, при параллельном соединении, будет одно и то же падение напряжения.

В соответствии с законом Ома, сопротивление нескольких последовательно соединенных резисторов равно:

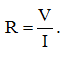(1)

Закон Кирхгофа для токов говорит нам, что ток, протекающий через данную цепь, будет равен сумме токов, протекающих через каждый из резисторов:

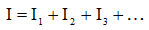(2)

Перепишем выражение (1) с учетом выражения (2):

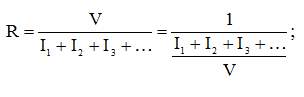
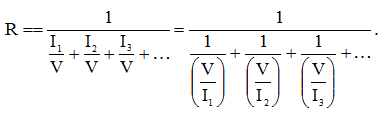(3)

Сопротивления каждого из резисторов определяются в соответствии с законом Ома:

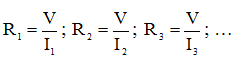(4)

С учетом соотношений (3) и (4) выражение для общего сопротивления двух параллельно соединенных резисторов примет окончательный вид:

 

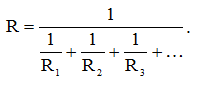
Упражнение 1.5

Покажите, что мощность, рассеиваемая на резисторе с сопротивлением более 1 кОм, не превысит четверти ватта, независимо от того, как вы его подключите к схеме, запитанной от источника, с постоянны напряжением 15 В.

В наличии: V_S = 15 В; R_min = 1 к Ом; R > R_min; P_max = 0,25 Вт.

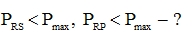
Прежде всего, установим связь между мощностью, напряжением и сопротивлением, так как именно этими величинами, судя по начальным данным, нам придется оперировать.

Мощность определяется в соответствии с общеизвестной формулой:

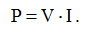(1)

По закону Ома, ток можно выразить в виде:

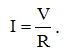(2)

Тогда с учетом выражения (2) формула для мощности (1) перепишется в виде:

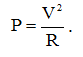(3)

Теперь рассмотрим подробнее последовательное и параллельное подключение нашего резистора к неизвестной нам схеме. Изобразим эту схему в виде «черного ящика» и для простоты будем полагать, что она состоит из резисторов.

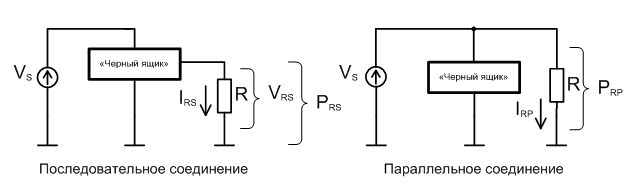
Теперь, согласно уравнению (3) мы можем выразить мощности, рассеиваемые на резисторе при последовательном и параллельном соединениях с «черным ящиком»:

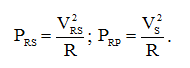(4)

Имея перед глазами рисунок и выражения (4), мы можем сделать справедливые выводы, что:

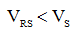(5)

и, следовательно

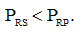(6)

 

Если мы рассмотрим последовательное соединение, то придем к заключению, что условие (5) верно, так как на цепях «черного ящика» будет наблюдаться некоторое падение напряжения.

Определим максимальную мощность при параллельном соединении, которая будет определяться все тем же уравнением (3):

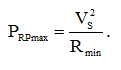
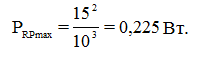(7)

Сравнивая полученное значение (7) со значением P_max (дается в условиях упражнения), мы можем записать:

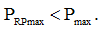(8)

Учитывая выражение (8) и то, что R > R_min, мы приходим к однозначному выводу:

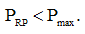(9)

Учитывая выражения (6) и (9) получаем, что:

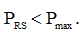
Таким образом, мы доказали, что не смотря на то, как подключается резистор к предложенной схеме, рассеиваемая на нем мощность не превысит четверти ватта.

 

Упражнение 1.6 (необязательное)

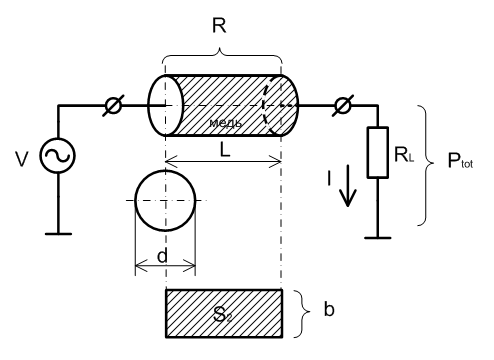
Нью-Йорку требуется примерно 10¹⁰ Вт электрической энергии при напряжении в электросети 115 В (это близко к истине: население в 10 миллионов жителей со средним потреблением электричества в 1 кВт на человека). Диаметр мощного силового кабеля линии электропередачи составляет 2,54 см. Давайте прикинем, что произойдет, если мы попытаемся передать необходимую городу электроэнергию по силовому кабелю длиной 1 м, состоящему из чистой меди. Удельное сопротивление меди составляет 1,7 мкОм ∙ см. Вычислите: а) потери мощности в предложенном куске кабеля (потери мощности определяются произведением I²R);

б) длину силового кабеля, на которой будет рассеяна вся необходимая городу мощность; в) как нагреется при этом 1 м кабеля, если вам не чужда физика

(σ = 6 ∙ 10^-12 Вт/(К⁴ ∙ см²)). Если ваши вычисления верны, то их  результаты вас озадачат. Как же разрешить возникшую проблему?

В наличии: P_tot = 10¹⁰ Вт; V = 115 В; d = 2,54 см; ρ = 1,7 ∙ 10^-6 Ом ∙ см; L = 1 м;

   σ = 6 ∙ 10^-12 Вт/(К⁴ ∙ см²).

а) P – ?

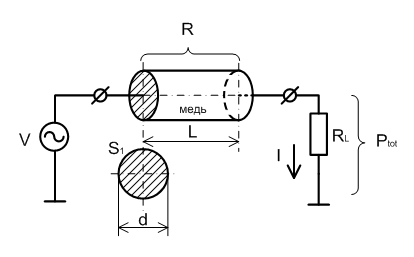
Мощность P, рассеиваемая куском силового кабеля, будет равна:

(1)

где V_R – падение напряжения на куске силового кабеля.

Ток через провод будет определяться нагрузкой R_L. Поэтому нам целесообразнее выразить мощность, рассеиваемую проводом, через величины тока и сопротивления.

В соответствии с законом Ома:

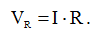(2)

Перепишем выражение (1) с учетом выражения (2):

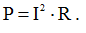(3)

Мы справедливо предполагаем, что падение напряжения на силовом кабеле незначительно. Поэтому, вся мощность должна передаваться нагрузке R_L (городским потребителям):

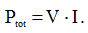(4)

С помощью выражения (4) мы можем определить ток I, протекающий в кабеле:

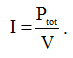(5)

Подставив (5) в (3) получим следующую формулу для мощности, рассеиваемой кабелем линии электропередачи:

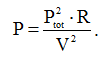(6)

Теперь определим сопротивление (R) силового кабеля, который представляет собой медный цилиндр. Из курса общей физики Вам должна быть известна формула, связывающая сопротивление проводника (R) с его удельным сопротивлением (ρ), площадью поперечного сечения (S₁) и длиной (L):

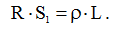(7)

Исходя из формулы (7) мы можем определить сопротивление силового кабеля, так как удельное сопротивление и длина нам известны, а площадь поперечного сечения мы можем вычислить:

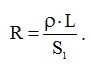(8)

Площадь поперечного сечения силового кабеля определяется формулой площади круга, известной из школьного курса геометрии, где вместо радиуса мы использовали диаметр (d):

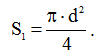(9)

Обобщим выражение для сопротивления силового кабеля, подставив (9) в (8):

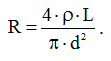(10)

Теперь мы можем записать общее выражение для мощности, рассеиваемой силовым кабелем, и рассчитать ее величину. Для этого подставим (10) в (6):

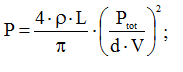(11)

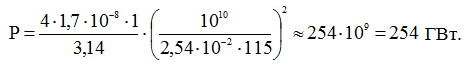
б) L_tot – ?

Если мы посмотрим на выражение (11), то увидим, что мощность (P), рассеиваемая силовым кабелем, прямо пропорциональна его длине (L). Поэтому, для определения длины кабеля (L_tot), на которой будет рассеиваться вся мощность (P_tot), необходимая городу, мы можем составить следующую пропорциональную зависимость:

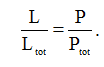(12)

Выражение (12) позволяет нам определить искомую величину и рассчитать ее:

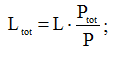
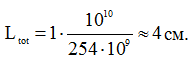
в) T – ?

Из курса общей физики известен закон Стефана-Больцмана для абсолютно черного тела. В нашем случае данный закон будет выражаться следующим образом:

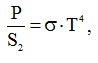(13)

где σ – постоянная Стефана-Больцмана; S₂ – излучающая поверхность силового кабеля.

Перепишем выражение (13) относительно искомой величины температуры:

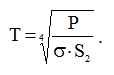(14)

Если «развернуть» боковую поверхность цилиндра силового кабеля, то окажется, что она представляет собой прямоугольник. Поэтому, площадь (S₂) будет равна:

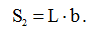(15)

Длина окружности (b) определяется по общеизвестной формуле, где вместо радиуса используется диаметр:

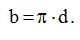(16)

Подставив (16) в (15) получим, что площадь излучающей поверхности равна:

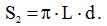(17)

Подставив (17) в (14), получим окончательное выражение и рассчитаем температуру кабеля:

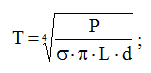(18)

 

Для сведения, температура плавления меди составляет 1358 ˚K!

Обобщая все произведенные нами расчеты, можно заключить, что мощность, рассеиваемая в одном метре силового кабеля электропередачи, превышает городскую потребность минимум на порядок. При этом этот метр кабеля нагревается до такой температуры, что должен не просто расплавиться, а испариться. В данном случае не может быть и речи об эффективной передаче электрической энергии.

Что же можно предпринять для решения сложившейся проблемы?

Нам, естественно, необходимо снизить рассеиваемую кабелем электропередачи мощность до разумных значений, которые будут определять приемлемую температуру кабеля. Если обратится к формуле (11), то мы можем увидеть, что параметров, которыми мы можем оперировать не так много: напряжение в сети и диаметр кабеля. Мы не можем применять слишком толстые кабели, так как они дороги и не технологичны, да и большого выигрыша в уменьшении потерь это не дает. А вот напряжение мы можем увеличить довольно сильно, благодаря повышающим напряжение трансформаторам. На практике так и поступают. На генерирующей станции повышают с помощью трансформаторов напряжение и передают по проводам электроэнергию до понижающего трансформатора, расположенного вблизи потребителя. Понижающий трансформатор возвращает напряжению номинальное значение.

Давайте прикинем, до какого значения нам необходимо увеличить напряжение, чтобы температура кабеля составила 300 ˚K. Перепишем выражение (18) относительно рассеиваемой мощности и определим ее:

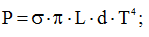
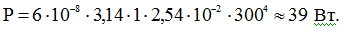
Теперь выражение (11) перепишем относительно напряжения и рассчитаем его:

 

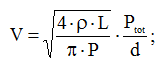
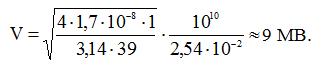
Данные расчеты мы произвели абстрактно для одного метра кабеля. В более сложном случае необходимо учитывать длину линии.

Замечания

Не случайно данное упражнение помечено как необязательное. Авторы рассчитывали, что его смогут решить лишь люди прошедшие общий курс физики. Но все усложнилось, потому, что в оригинальном втором издании книги поселились ошибки и опечатки в задании упражнения. Эти же ошибки и опечатки перекочевали практически без изменения и в третье оригинальное издание. Причем, они не обозначены как найденные даже на сайте поддержки книги. На наших же соотечественников легла двойная тяжесть, так как переводчики второго издания особо не вдавались в физический смысл и не смогли исправить допущенные авторами оплошности. В оригинальном тексте используются так любимые американцами дюймы и футы в качестве мер длины. С учетом всего изложенного выше, я взял на себя смелость переработать текст упражнения, откорректировать и адаптировать его для отечественного читателя.

Данное упражнение дает лишь общие представления о процессах, происходящих в линиях электропередачи и не более того.