Упражнения 1.10, 1.11, 1.12, 1.13 "Искусство схемотехники", 3-е издание

Упражнение 1.10

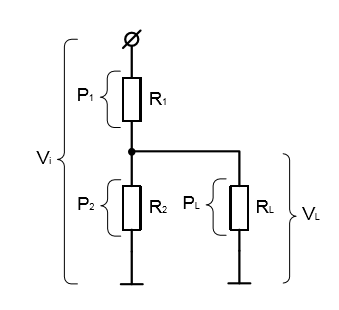
Дана схема, изображенная на рисунке 1.12, со следующими параметрами:

V_i = 30 В; R₁ = R₂ = 10 кОм. Необходимо определить: а) напряжение на выходе без нагрузки (напряжение холостого хода); б) напряжение на выходе с подключенной нагрузкой в 10 кОм (изобразите в виде делителя напряжения, у которого R₂ и R_L представлены одним резистором); в) эквивалентную схему Тевенина; г) то же, что и в пункте б), но с применением эквивалентной схемы Тевенина (вы снова имеете дело с делителем напряжения; ответ должен совпадать с ответом к пункту б)); д) мощность, рассеиваемую каждым из резисторов.

В наличии: V_i = 30 В; R₁ = R₂ = 10 кОм; R_L = 10 кОм.

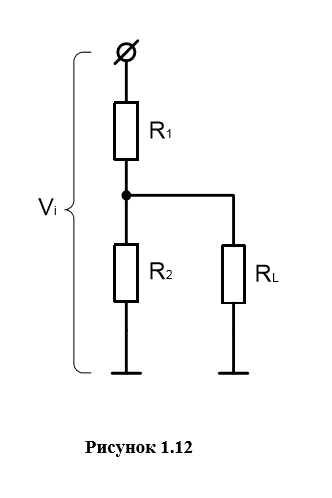
а) V_o – ?

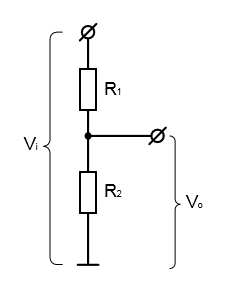
Из ранее пройденного материала книги, нам известно, что выходное напряжение (напряжение холостого хода) для делителя напряжения, образованного резисторами R₁ и R₂, будет определяться и рассчитываться в соответствии со следующим выражением:

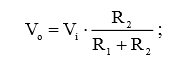(1)

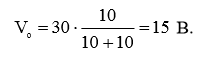(2)

б) V_L – ?

Так как R₂ = R_L, то их общее сопротивление будет равно:

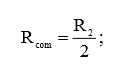
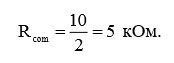
Снова имеем дело с делителем напряжения. Поэтому, для расчета выходного напряжения при подключенной нагрузке, воспользуемся формулой выходного напряжения делителя напряжения:

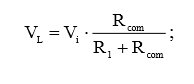
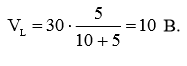
в)  V_Th – ?; R_Th – ?

В соответствии с методикой, описанной в книге, определяем параметры эквивалентной схемы Тевенина.

Напряжение эквивалентного источника питания будет равно выходному напряжению холостого хода делителя (1), (2):

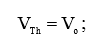(3)

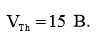(4)

Ток, при коротком замыкании выхода делителя, по закону Ома будет равен:

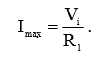(5)

По закону Ома последовательное сопротивление эквивалентного источника питания будет равно:

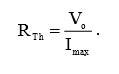(6)

Подставив в выражение (6) выражение (5), получим окончательную формулу для искомой величины и рассчитаем ее с помощью полученного ранее значения (4):

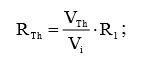
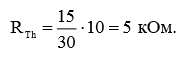(7)

г) V_L – ?

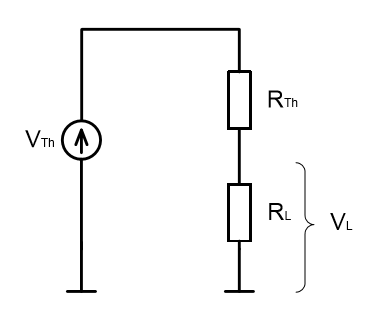
Параметры  эквивалентной схемы  Тевенина (4) и (7) мы рассчитали в предыдущем пункте упражнения.

В результате применения эквивалентной схемы Тевенина у нас получился делитель напряжения, поэтому напряжение на его выходе будет равно:

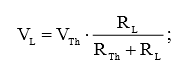
Как видите, ответ тот же, что и в пункте б) данного упражнения.

д) P₁ – ?; P₂ – ?; P_L – ?

В общем случае, применив закон Ома, мощность можно выразить через величины напряжения и сопротивления:

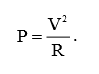(8)

Используя рисунок, результаты предыдущих вычислений и формулу (8), мы легко рассчитаем искомые мощности:

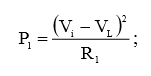
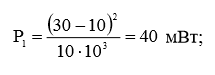
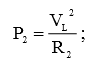
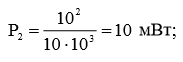
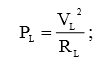
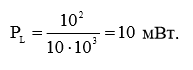
Упражнение 1.11

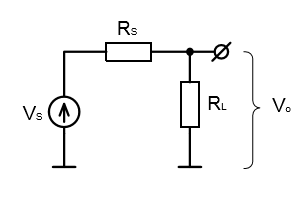
Покажите, что при равенстве сопротивления нагрузки сопротивлению источника питания (R_L = R_S), мощность, рассеиваемая в нагрузке, максимальна. Замечание: пропустите данное упражнение, если вы не представляете себе его решения и просто примите на веру, что приведенное утверждение справедливо.

В наличии: P_L = max; V_S = const.; R_S = const.

{R_L = R_S} – ?

Мощность, рассеиваемую нагрузкой, можно выразить через величины напряжения и сопротивления:

(1)

Наша схема представляет собой делитель напряжения, поэтому ее выходное сопротивление будет определяться следующим выражением:

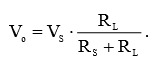(2)

Подставив выражение (2) в выражение (1), получим мощность, представленную в виде функции от переменной, которой является сопротивление нагрузки:

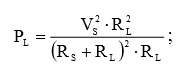
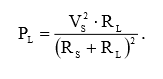(3)

Из курса математики известно, что любую функцию можно исследовать на экстремум. Воспользуемся же этой возможностью. Для этого необходимо взять производную функции (3) по переменной R_L:

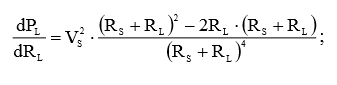
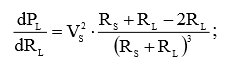
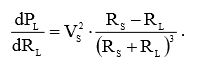(4)

Я не стал приводить законы дифференциального исчисления, которые применялись для вывода выражения (4), так как они общеизвестны и содержатся в математических справочниках.

В точке максимума функции, производная должна быть равна нулю:

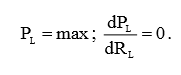
Поэтому, приравняем выражение (4) к нулю и определим условие максимума:

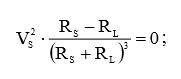
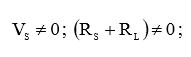
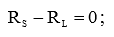
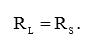
Упражнение 1.12

Определите отношения напряжений и мощностей для двух сигналов, которые заданны в децибелах: а) 3 дБ; б) 6 дБ; в) 10 дБ; г) 20 дБ.

В наличии: а) k_V = k_P = 3 дБ;  б) k_V = k_P = 6 дБ; в) k_V = k_P = 10 дБ;

   г) k_V = k_P = 20 дБ.

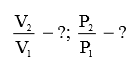
Относительный коэффициент передачи напряжения определяется по формуле:

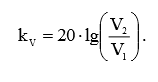(1)

Выполнив над формулой (1) ряд элементарных математических преобразований, получим выражение для расчета искомой величины отношения напряжений двух сигналов (или абсолютного коэффициента передачи напряжения):

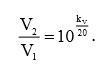(2)

Относительный коэффициент передачи мощности определяется по формуле:

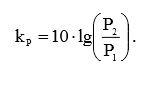(3)

Выполнив над формулой (3) те же преобразования, что и над формулой (1), получим выражение для расчета искомой величины отношения мощностей двух сигналов (или абсолютного коэффициента передачи мощности):

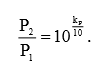(4)

Для каждого из пунктов будем производить вычисления в соответствии с формулами (2) и (4).

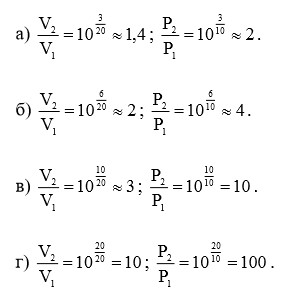
Для наглядности, занесем результаты наших вычислений в сводную таблицу.

Упражнение 1.13

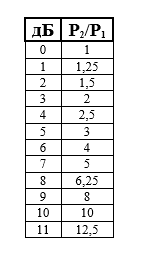
Мы можем назвать это занимательное упражнение «Пустынный остров децибел». В таблице, представленной ниже, мы начали вводить некоторые значения отношений мощностей двух сигналов, заданных в децибелах для двенадцати целочисленных значений, используя результаты, полученные при решении  предыдущего упражнения в пунктах а) и в). Вы должны закончить заполнение данной таблицы без использования калькулятора. Подсказка: начните со значения «10 дБ» и опускайтесь по таблице с шагом 3 дБ, пока не упретесь; затем поднимитесь с шагом 10 дБ и снова опускайтесь с шагом 3 дБ. Не усложняйте себе задачу и не прибегайте к излишней точности: округляйте полученные значения до приемлемых величин.

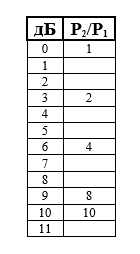
Итак, из предыдущего упражнения нам известно, что 3 дБ – это (P₂/P₁) = 2 и

10 дБ – это (P₂/P₁) = 10.

Воспользуемся подсказкой, и опустимся на 3 дБ со значения «10 дБ». Мы оказываемся у значения «7 дБ». Отношение мощностей при этом должно уменьшиться в два раза и составить величину, равную 5.

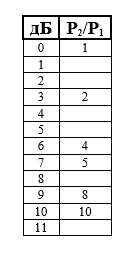
Снова опускаемся со значения «7 дБ» на 3 дБ. Оказываемся напротив значения «4 дБ». Значение отношения мощностей снова уменьшается в два раза и равно 2,5.

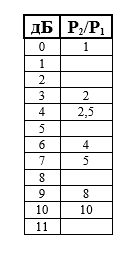
Опускаемся со значения «4 дБ» на 3 дБ. Оказываемся напротив значения «1 дБ». Значение отношения мощностей уменьшается в два раза и составляет 1,25.

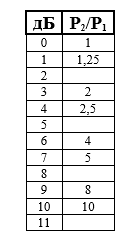
Теперь поднимаемся со значения «1 дБ» на 10 дБ. И оказываемся напротив значения «11 дБ». Значение отношения мощностей увеличивается в десять раз и составляет 12,5.

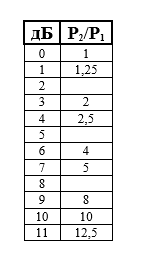
Вновь опускаемся со значения «11дБ» на 3 дБ. Оказываемся напротив значения «8 дБ». Значение отношения мощностей уменьшается в два раза и составляет 6,25.

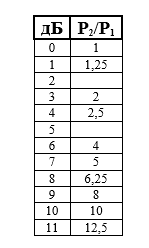
Опускаемся со значения «8 дБ» на 3 дБ. Оказываемся напротив значения «5 дБ». Значение отношения мощностей уменьшается в два раза и составляет примерно 3.

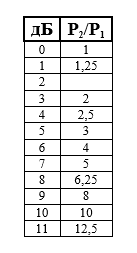
И, наконец, опускаемся со значения «5 дБ» на 3 дБ. Оказываемся напротив значения «2 дБ». Значение отношения мощностей уменьшается в два раза и составляет примерно 1,5.