Упражнение 1.41
Как можно было бы сконструировать фильтр из резисторов и конденсаторов, чтобы получить для него характеристику, изображенную на рисунке 1.136?
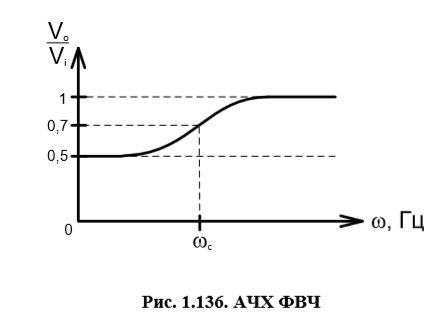
В наличии: R = const.; C = const.; ωс = const.
Составить схему.
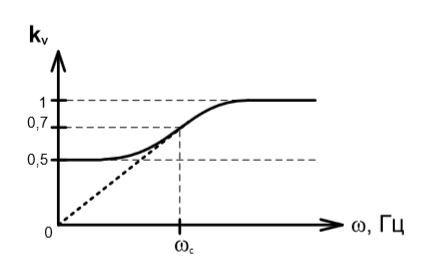
Рассмотрим АЧХ фильтра. На высоких частотах схема ведет себя как фильтр высоких частот (ФВЧ). На низких частотах сигнал делится пополам. Очевидно, что наша схема будет иметь следующий вид.
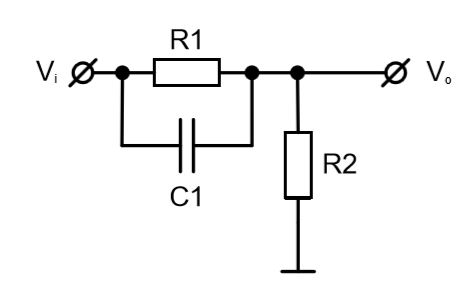
На низких частотах схема ведет себя как резистивный делитель с коэффициентом передачи по напряжению, равным:
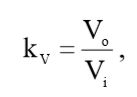
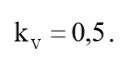 (1)
(1)
На низких частотах реактанс конденсатора С1 больше сопротивления резистора R1, поэтому, коэффициент передачи делителя на резисторах R1 и R2 будет определяться общеизвестной формулой:
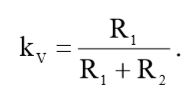 (2)
(2)
Приравняв (1) и (2) получим соотношение номиналов резисторов:
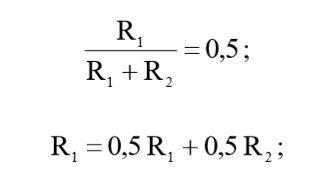
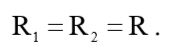 (3)
(3)
Емкость конденсатора С1 можно принять равной:
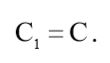 (4)
(4)
На высоких частотах реактанс конденсатора С1 меньше сопротивления резистора R1, иными словами конденсатор шунтирует резистор и схема ведет себя как простой RC-фильтр высоких частот. Как нам уже известно, угловая частота среза по уровню «-3 дБ» в этом случае будет определяться следующим выражением:
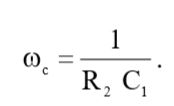 (5)
(5)
С учетом (3) и (4) выражение (5) примет окончательный вид:
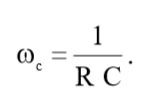
Упражнение 1.42
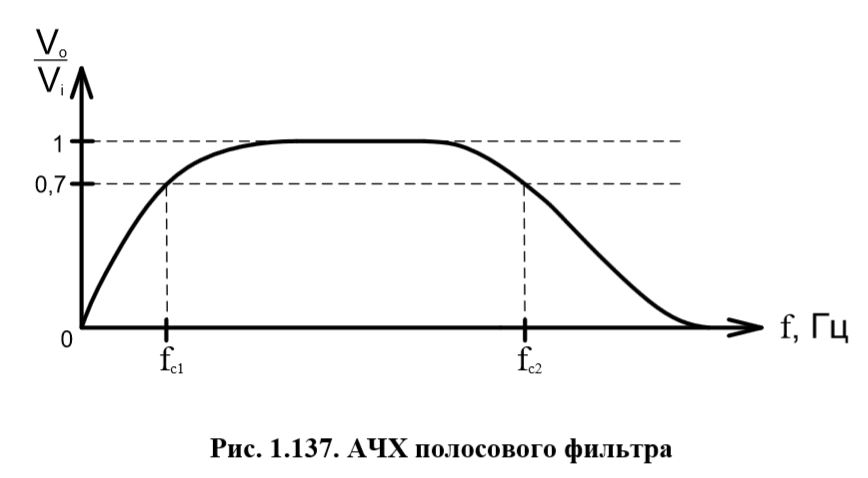
Разработайте полосовой RC-фильтр ( в соответствии с характеристикой рисунка 1.137). Частоты fc1 и fc2 принять по уровню «-3 дБ». Выбрать импедансы так, чтобы второй каскад оказывал незначительное влияние на первый каскад в качестве нагрузки.
В наличии: |ZL|min = const.; fc1 = const.; fc2 = const.
Составить схему.
Так как числовые данные отсутствуют, то упражнение будет решаться в общем виде.
Расчет будет производиться с помощью комплексных величин, как и описано в книге. Поэтому, для полного понимания предмета, следует предварительно прочесть Приложение А книги по теме комплексных чисел.
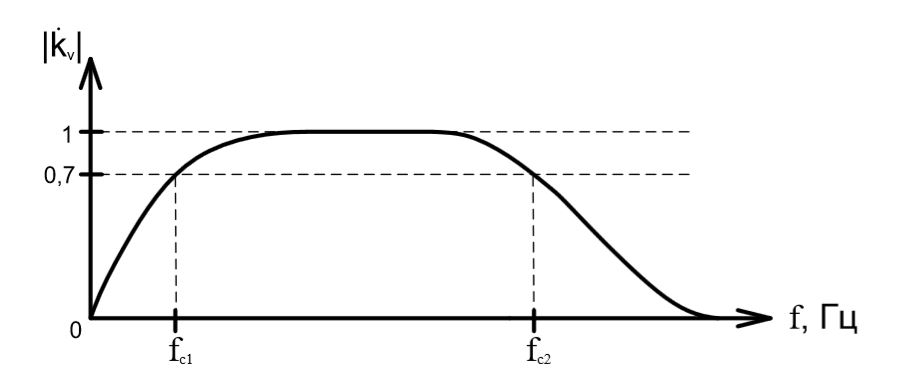
Благодаря книге нам известен внешний вид амплитудно-частотных характеристик фильтров низких и высоких частот. Учитывая условия упражнения и внешний вид прилагаемой амплитудно-частотной характеристики полосового фильтра, не трудно догадаться, что наша схема будет состоять из последовательно соединенных фильтра низких частот и фильтра высоких частот (в любой последовательности).
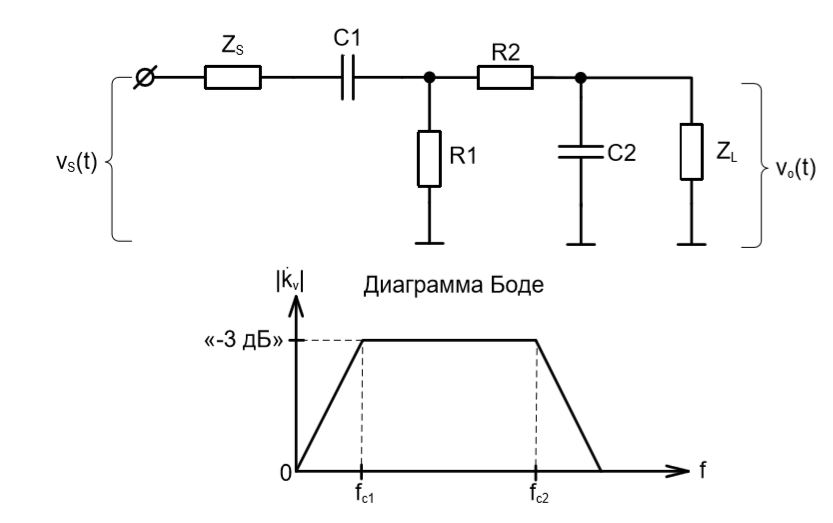
Рассмотрим выходной каскад нашего устройства в виде фильтра низких частот (на компонентах R2 и C2) и применим к нему следствия из теоремы Тевенина для RC-фильтров, которые мы вывели в упражнении 1.23.
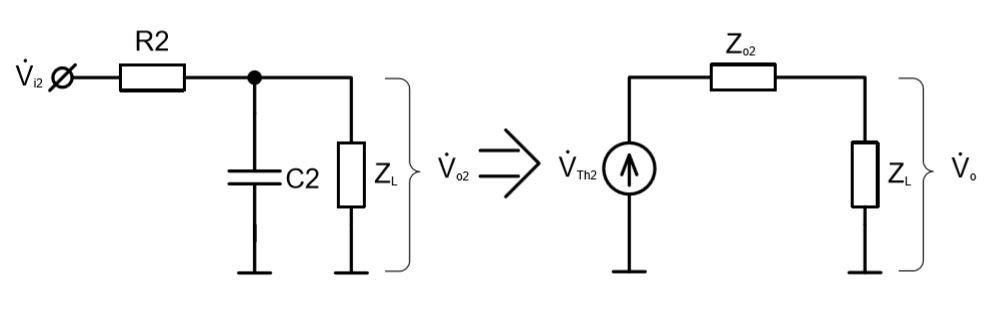
Вспомним, что для простого RC-фильтра максимальная величина выходного импеданса будет равна (см. упражнение 1.23):
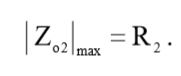 (1)
(1)
Чтобы влияние нагрузки было минимально допустимым, достаточно выполнения условия для выходного импеданса фильтра:
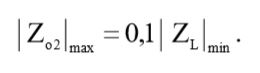 (2)
(2)
Приравняв (1) и (2) мы получим номинал резистора R2 с учетом минимальной величины импеданса нагрузки:
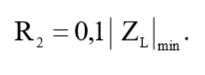 (3)
(3)
Нам уже известно, что для RC-фильтра частота среза по уровню «-3 дБ» равна:
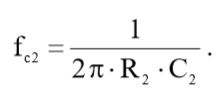 (4)
(4)
С помощью формулы (4) выразим искомую емкость и рассчитаем ее, подставив исходные данные и результат вычислений (3):
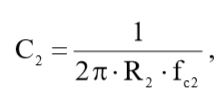
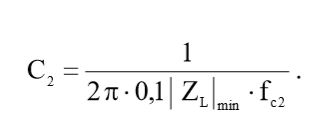 (5)
(5)
Теперь рассмотрим соединение первого и второго каскадов нашего фильтра (ФВЧ и ФНЧ).
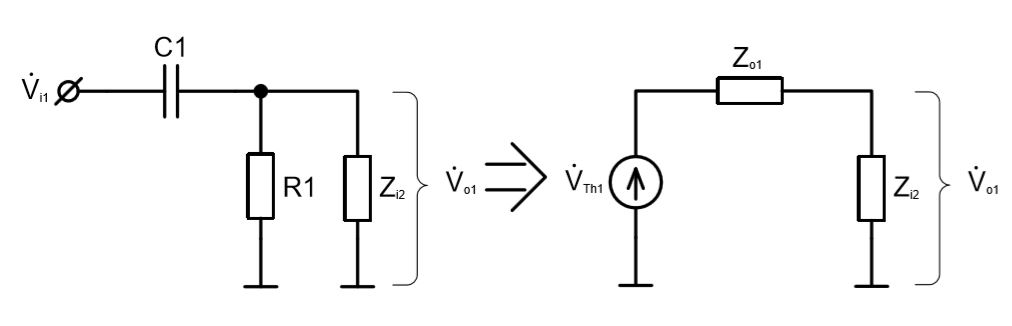
В соответствии с выводами, сделанными в упражнении 1.23, величина минимального входного импеданса фильтра низких частот будет равна:
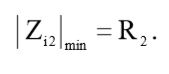 (6)
(6)
Чтобы влияние фильтра низких частот на выходное напряжение фильтра высоких частот было минимально допустимым, достаточно выполнения условия для величины выходного импеданса фильтра ФВЧ:
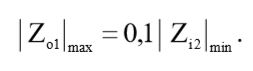 (7)
(7)
Подставив (6) в (7), мы получим:
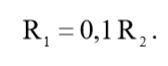 (8)
(8)
В соответствии с выводами, сделанными в упражнении 1.23, максимальная величина выходного импеданса фильтра высоких частот будет равна:
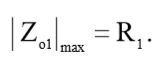 (9)
(9)
Подставив (8) в (9), мы получим выражение для определения номинала резистора R1:
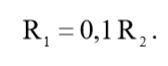 (10)
(10)
Подставив (3) в (10), мы получим окончательное выражение:
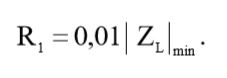 (11)
(11)
Частота среза по уровню «-3 дБ» для фильтра высоких частот равна:
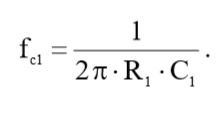 (12)
(12)
С помощью формулы (12) выразим искомую емкость и рассчитаем ее, подставив исходные данные и результат вычислений (11):
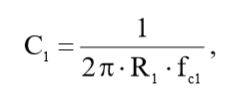
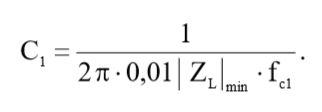 (13)
(13)
В заключение, рассмотрим делитель, образованный выходным импедансом источника сигнала и входным импедансом фильтра высоких частот.
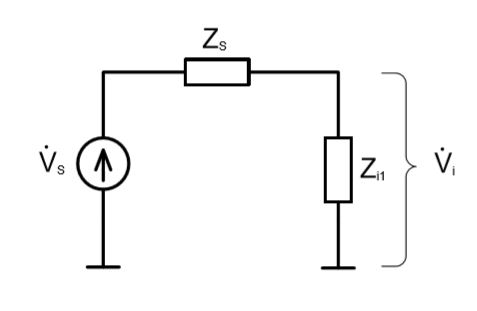
В соответствии с выводами, сделанными в упражнении 1.23, минимальная величина входного импеданса фильтра высоких частот будет равна:
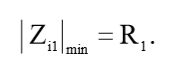 (14)
(14)
С учетом выражения (11), перепишем выражение (14):
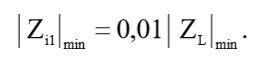 (15)
(15)
Чтобы влияние фильтра высоких частот на источник сигнала было минимально допустимым, достаточно выполнения условия для величины выходного импеданса источника сигнала:
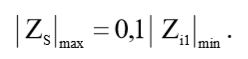 (16)
(16)
Подставив в выражение (15) формулу (16), мы получим окончательное выражение для выходного импеданса источника сигнала:
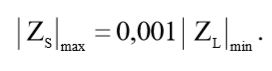 (17)
(17)
В результате наших вычислений мы получили ряд расчетных формул для нашего полосового фильтра в виде выражений (3), (5), (11), (13) и (17).
Замечание
Пример «прямого» расчета (исходя из характеристик источника сигнала) полосового фильтра приведен в упражнении 1.24.
Упражнение 1.43
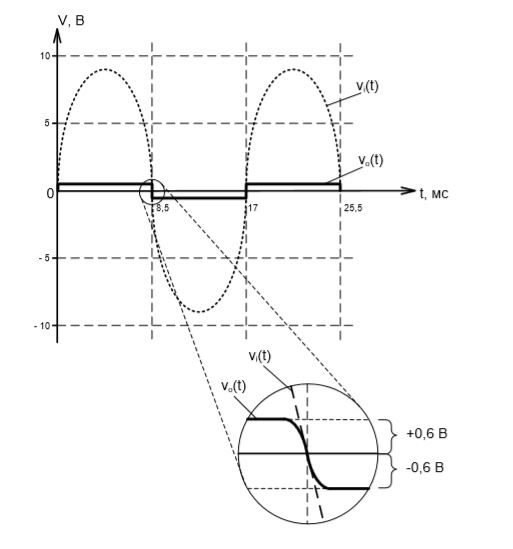
Зарисуйте выходной сигнал для схемы, изображенной на рисунке 1.138.
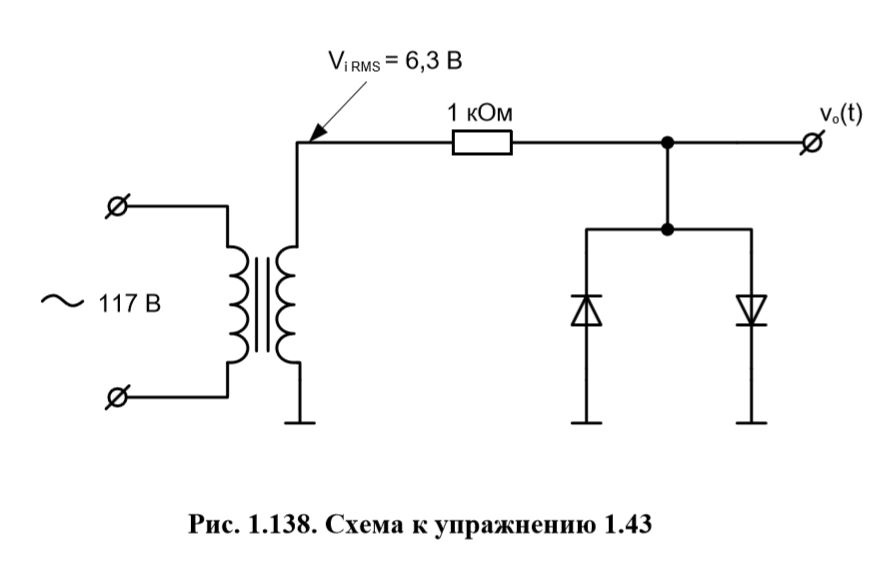
В наличии: R = 1 кОм; VRMS = 117 В; f = 60 Гц; Vi RMS = 6,3 В; VD = 0,6 В.
vo(t) – ?
Зарисовать выходной сигнал схемы.
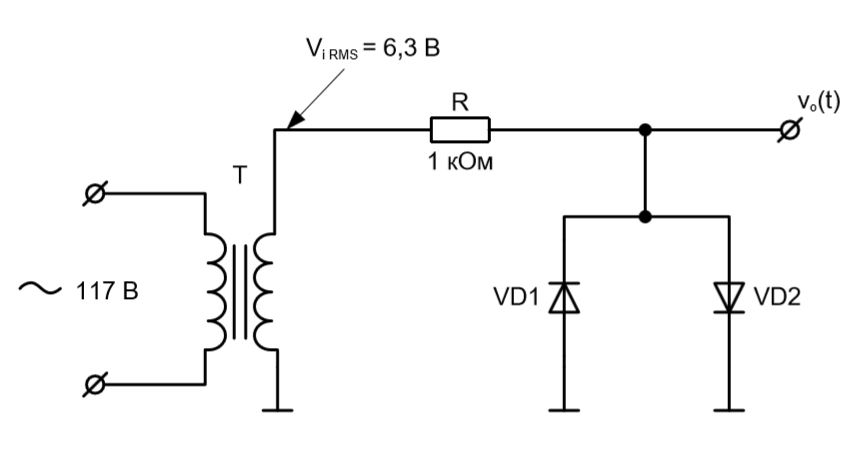
Как вы должны были догадаться, перед нами схема симметричного диодного ограничителя напряжения.
Принцип действия ее следующий.
Вся схема питается от источника переменного напряжения промышленной частоты, соответствующего стандарту США, через понижающий трансформатор T. На вторичной обмотке трансформатора T формируется сниженное напряжение синусоидальной формы vi(t), той же частоты, что и питающее напряжение. Затем, напряжение vi(t) подается на выход схемы через резистор R, выступающий в роли токового ограничителя. Диоды VD1 и VD2 в работе схемы не принимают участия до тех пор, пока напряжение на вторичной обмотке трансформатора не станет больше (или меньше) порогового напряжения ограничения, роль которого в нашем случае выполняет прямое падение напряжения на диоде VD. За ограничение положительной полуволны отвечает диод VD2, а за ограничение отрицательной полуволны – диод VD1.
Прежде, чем зарисовать выходной сигнал схемы, нам следует построить сигнал, формируемый на вторичной обмотке трансформатора T. Мы уже знаем, что этот сигнал имеет синусоидальную форму: осталось только вычислить его характеристики в соответствии с исходными данными.
Амплитуда напряжения на вторичной обмотке связана с действующим значением напряжения Vi RMS на вторичной обмотке следующей общеизвестной формулой:
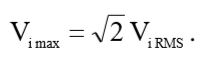 (1)
(1)
Вычислим значение амплитуды по формуле (1):
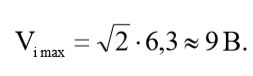 (2)
(2)
Период колебаний обратно пропорционален частоте сигнала:
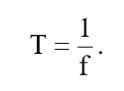 (3)
(3)
Вычислим значение периода колебаний по формуле (3):
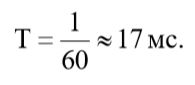 (4)
(4)
Теперь, зная параметры сигнала на вторичной обмотке трансформатора T (см. значения (2) и (4)), мы можем построить его на графике вместе с напряжением на выходе схемы.
Упражнение 1.44
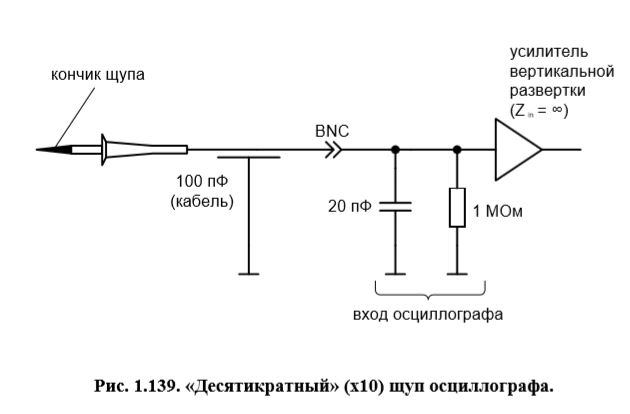
Разработайте «десятикратный» (x10) щуп осциллографа для использования с прибором, входной импеданс которого состоит из сопротивления в 1 МОм и параллельно с ним соединенной емкости в 20 пФ. Прикиньте в уме, что при этом должно содержаться в ручке щупа, изображенного на рисунке 1.139. Считайте, что соединительный кабель щупа вносит еще 100 пФ дополнительной емкости. Все компоненты щупа расположены на соединительном кабеле со стороны острого наконечника щупа (а не со стороны осциллографа). Получившаяся схема должна давать ослабление сигналов в 20 дБ (ослабление напряжения в 10 раз) на всех частотах, включая и сигналы постоянного тока. «Десятикратный» щуп применяется для уменьшения эффекта нагрузки, обусловленного подключением осциллографа к тестируемой схеме. Какой входной импеданс (параллельное соединение сопротивления Ri и емкости Ci ) обеспечит ваш «десятикратный» щуп при подключении тестируемой схемы к осциллографу?
В наличии: Ri osc = 1 MОм; Ci osc = 20 пФ; Ccab = 100 пФ;
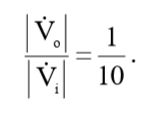 (1)
(1)
R – ? C – ? Ri – ? Ci – ? |Zi| – ?
Вычисления будут производиться с помощью комплексных величин, как и описано в книге. Поэтому, следует предварительно прочесть Приложение А книги по теме комплексных чисел.
Исходя из того, что мы уже знаем о свойствах резистивного делителя напряжения, а также из тех сведений, что содержатся в тексте упражнения, мы можем смело утверждать: в ручке «десятикратного» щупа содержатся параллельно соединенные резистор и конденсатор. Исходя из этого, перерисуем схему с Рис. 1.139.
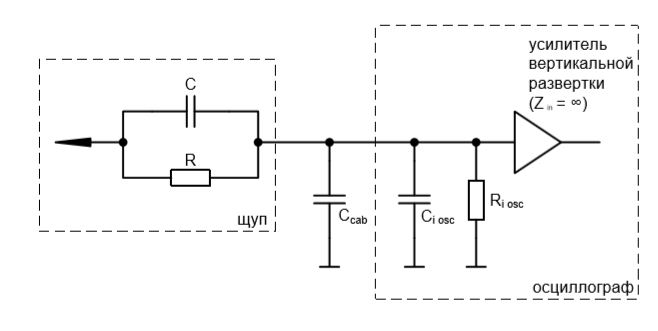
Емкость кабеля и входная емкость осциллографа включены параллельно, поэтому их общая емкость будет равна:
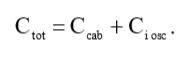 (2)
(2)
Вычисляем по формуле (2) общую емкость:
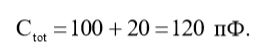 (3)
(3)
Article2
Перерисуем схему с учетом выражения (2).

В результате у нас получился «импедансный» делитель напряжения.
По аналогии с резистивным делителем, комплексный коэффициент передачи по напряжению будет равен:
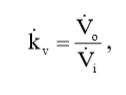 (4)
(4)
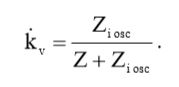 (5)
(5)
Применив теорему Тевенина к последней схеме, мы можем определить входной импеданс по отношению к измеряемой схеме.
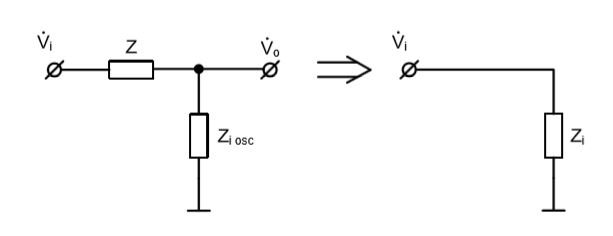
В соответствии с данной схемой, входной импеданс по отношению к измеряемой схеме, будет равен:
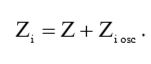 (6)
(6)
С учетом (6), выражение (5) примет вид:
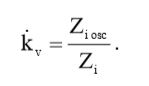 (7)
(7)
В соответствии с выражением (4), величина комплексного коэффициента передачи по напряжению будет равна:
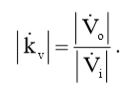 (8)
(8)
В связи с выражением (8), условие (1) примет следующий вид:
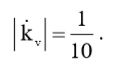 (9)
(9)
Вернувшись к выражению (7) и учитывая условие (9), мы можем записать:
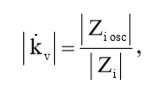 (10)
(10)
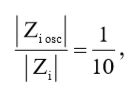
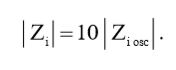 (11)
(11)
Выражение (11) раскрывает нам суть применения «десятикратного» щупа. «Десятикратный» щуп увеличивает в 10 раз входной импеданс измерительной схемы по отношению к измеряемой схеме, тем самым, уменьшая влияние первой на последнюю.
Рассмотрим теперь детально импеданс резистора R и конденсатора С, размещенных в ручке «десятикратного» щупа.
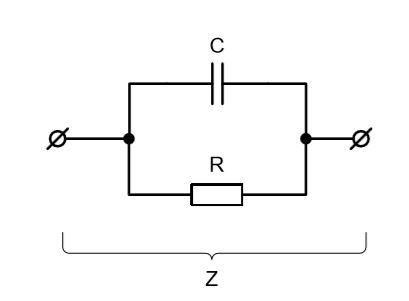
Импеданс Z будет равен:
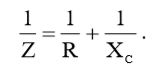 (12)
(12)
Реактанс конденсатора C равен:
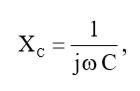 (13)
(13)
где
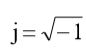 – мнимая единица,
– мнимая единица,
ω – угловая частота сигнала.
Подставив (12) в (13), получим выражение для импеданса Z:

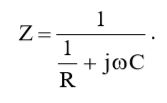 (14)
(14)
Рассмотрим теперь входной импеданс осциллографа с учетом емкости кабеля, соединяющего его с щупом.
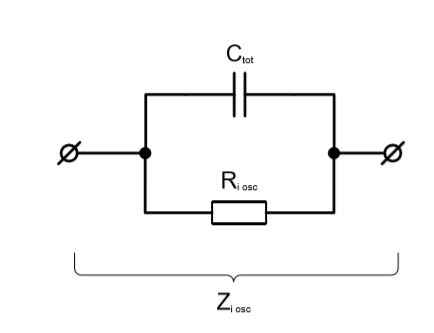
По аналогии с выражением (14), входной импеданс осциллографа будет равен:
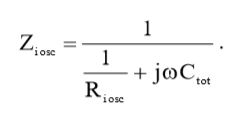 (15)
(15)
Подставив (14) и (15) в выражение (6), мы получим:
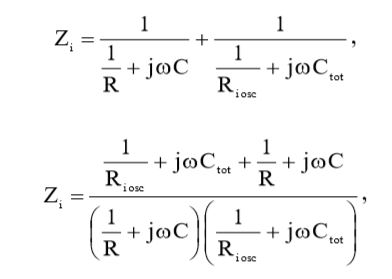
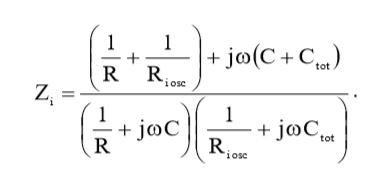 (16)
(16)
Подставив (15) и (16) в выражение (7), мы получим окончательное выражение для комплексного коэффициента передачи по напряжению:
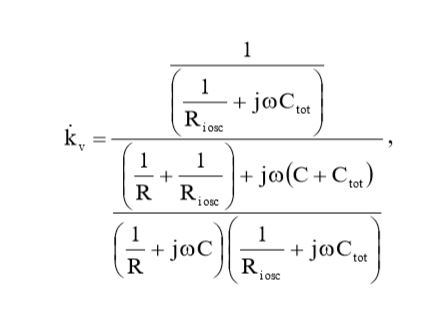
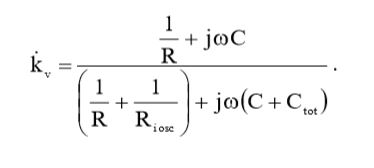 (17)
(17)
Применив выражение (17) в условии (9), мы получим:
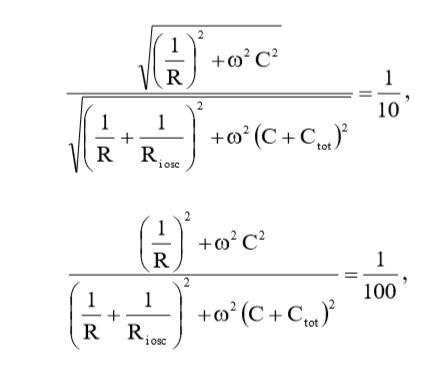
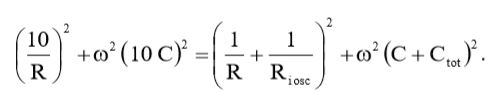 (18)
(18)
Используя равенство (18), мы можем записать:
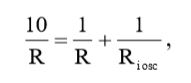 (19)
(19)
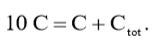 (20)
(20)
Воспользовавшись выражением (19), мы можем вычислить сопротивление резистора R:
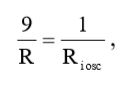
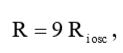 (21)
(21)
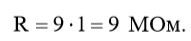
Воспользовавшись выражением (20) и результатами вычислений (3), мы можем вычислить емкость конденсатора C:
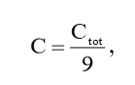 (22)
(22)
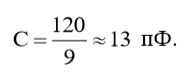
Теперь, если мы вернемся к выражению (11) для величины входного импеданса и учтем выражение (15), то в итоге мы получим:
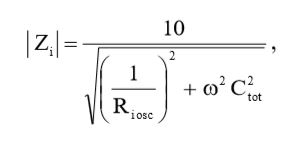
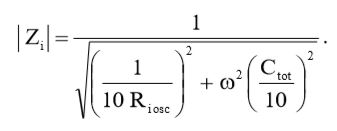 (23)
(23)
Так как наша схема состоит исключительно из резисторов и конденсаторов, то мы совершенно справедливо можем представить входной импеданс в виде параллельно соединенных резистора и конденсатора.
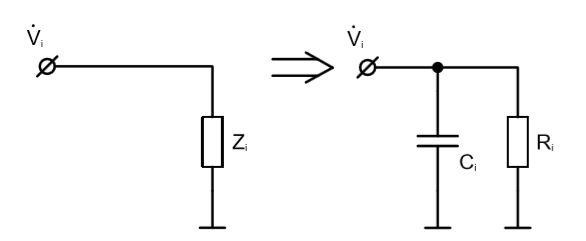
По аналогии с выражением (14), входной импеданс будет равен:
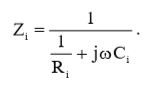 (24)
(24)
В соответствии с формулой (24), величина входного импеданса равна:
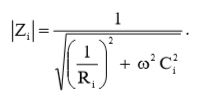 (25)
(25)
Приравняв (25) и (23), получим искомые величины:
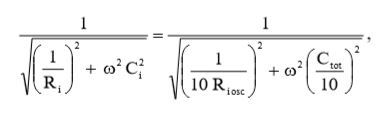
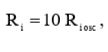 (26)
(26)
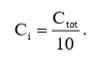 (27)
(27)
Рассчитаем по формуле (26) величину входного сопротивления:
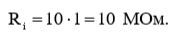
Рассчитаем по формуле (27) величину входной емкости:
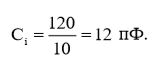











 Опубликована:
Опубликована:


 Вознаградить
Вознаградить




Комментарии (4) |
Я собрал (0) |
Подписаться
|
Я собрал (0) |
Подписаться
Для добавления Вашей сборки необходима регистрация
[Автор]