Дополнение Б - Представление чисел

Представление чисел в позиционной системе исчисления

Любое n-разрядное число K в позиционной системе может быть представлено в виде следующего полинома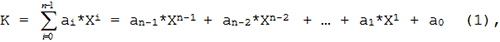

где ai – весовые коэффициенты при соответствующих разрядах, X – основание системы.

Основание системы определяет количество чисел, которое используется в системе исчисления. Коэффициенты a_i могут быть представлены только числами из этого набора. Например, в двоичной системе (основание X=2), используются числа 0 и 1, в десятичной (X=10) – 0…9, в шестнадцатеричной (X=16) – 0…9 и символы A,B,C,D,E,F.

Двоичная система исчисления является доминирующей в вычислительной технике. Она наиболее удобна для обработки данных, представленных на уровне электрических сигналов. Полином (1) в этом случае имеет вид
K = a_n-1*2^n-1 + a_n-2*2^n-2 + … + a₁*2¹ + a₀.

Двоичные числа могут отражать до 2ⁿ уникальных комбинаций и, соответственно, предоставляют диапазон изменения переменных 0…2^n-1. Так для 8-разрядных чисел это 0…255_­10, для  16-разрядных - 0…6553₁₀ и т.д. (индексы 2,10,16 в обозначениях чисел используется как показатель основания системы).

В табл.1 приведен пример записи чисел в трех различных системах исчисления.

Табл.1. Числа в различных системах исчисления.

Представление чисел в дополнительном коде

Дополнительный код это наиболее распространенная форма представления знаковых чисел. Диапазон изменения чисел для n-разрядных данных в двоичной системе -2^n-1…2^n-1-1.

Представление неотрицательных чисел в дополнительном коде (см. табл.2) совпадает с соответствующим представлением чисел в позиционной системе. Отрицательные же числа в дополнительном коде получаются в результате следующего действия
- X = 2ⁿ – X  (2).

 Выражение (2) может быть записано также в следующем виде
- X = 2^n-1 – X + 1 .   

Из-за этого дополнительный код иногда называют “дополнение до двух” (2^n-1 – X - действие инверсии или “дополнение до одного” и +1 – действие “дополнение до двух”).
Так, например, можно изменить знак 1-байтового числа 95₁₀ на противоположный 
95₁₀­ = 01011111₂ = 5F₁₆
- 95_10­ = 11111111₂ - 1011111₂ + 1₂ = 10100001₂ = A1₁₆

Старший разряд в дополнительном коде всегда является показателем знака числа (знаковый разряд). У положительных чисел MSB=0, а у отрицательных - MSB=1. Модуль наибольшего положительного числа на единицу меньше модуля наименьшего отрицательного числа.

Табл.2. Представление чисел в дополнительном коде.

Двоично-десятичное кодирование

Для хранения десятичных чисел часто используется двоично-десятичное кодирование (ДДК). В этом случае байты разбиваются на тетрады, в каждой из которых размещаются двоично-кодированные десятичные числа. Например, числу 10010110­₂ в ДДК соответствует десятичное число 96₁₀ (1001­₂ = 9₁₀ – старший полубайт, 0110­₂ = 6₁₀ – младший полубайт).

ДДК применяется в основном для представления пользовательской информации в удобной и понятной для человека десятичной системе исчисления. Однако формат ДДК позволяет хранить в одном байте только 100 десятичных чисел (числа 0…99₁₀). И, кроме того, далеко не каждый микропроцессор имеет в своей системе команды для обработки чисел в ДДК (в частности, у микроконтроллеров AVR такие команды отсутствуют).

Представление чисел в форме с фиксированной запятой

Если полином из (1) умножить на X^-m, где m неотрицательное целое число, то получим выражение для представления чисел с фиксированной запятой: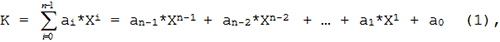

Числа такого типа содержат две части: целую и дробную. Под целую часть отводиться n-m разрядов, а под дробную m разрядов. Естественно, что в случае m=0 дробная часть отсутствует и (3) переходит формулу (1).

Например, 8-разрядное двоичное число K с m=4 будет иметь вид
 K =a₇*2³ + a₆*2² + a₅*2¹ + a₄*2⁰ + a₃*2^-1 + a₂*2^-2 + a₁*2^-3 + a₀*2^-4 (3).

Разряды a₇a₆a₅a₄ представляют собой целую часть числа, а a3a2a1a0 – дробную.

Формат чисел с фиксированной запятой имеет обозначение (N.Q), где N и Q число целых и дробных разрядов соответственно. Так в предыдущем примере число K имеет формат (4.4).

При программировании 8-разрядных микроконтроллеров на ассемблере в подобной форме представления, как правило, нет необходимости. Однако числа с фиксированной запятой имеют определенные преимущества при цифровой обработке сигналов в специализированных DSP (Digital Signal Processor) процессорах, где их поддержка введена аппаратном уровне.

Представление чисел в форме с плавающей запятой

Числа с плавающей запятой имеют экспоненциальную форму записи, при которой отдельно представляются мантисса и порядок числа.    
K = M * 2 ^E,

где M – мантисса, E – порядок.

Таким образом, числа с плавающей запятой должны отображаться в ОЗУ микропроцессора в виде двух частей, каждая из которых может иметь соответствующее число разрядов (чаще всего кратное 8).

Как M, так и E, могут быть знаковыми числами. Мантисса должна быть представлена в виде числа с фиксированной запятой и находиться в пределах 0≤|m|≤1, а порядок M – виде целого числа.

Для повышения точности представления чисел разрядность M требуется всегда выше, чем разрядность E. Диапазон же представления чисел практически полностью определяется разрядностью E.

Программирование математических операций над числами с плавающей запятой связано со значительными трудностями и требует большого расхода памяти программ и данных. К счастью такой формат является избыточным для подавляющего большинства приложений, где используются 8-разрядные микроконтроллеры, и в основном встречается только в некоторых задачах управления и фильтрации. Числа с плавающей запятой иногда также применяют для создания и пересылки архивов данных в компьютер.

Представление символьной информации в кодировке ASCII

ASCII (American Standard Code for Information Interchange) – общепринятый стандарт кодирования информации. В соответствии с ним каждому символу из табл.3 сопоставляется индивидуальный 7-разрядный числовой код. Таблица разделена на 128 частей, но реально, только диапазону адресов 0x20…0x7E соответствует информация, которая воспринимается, как символьная. Остальные кода, размещенные по адресам 0x00…0x1F и 0x7F, отведены командам управления. Большинство из них поддерживает любая терминальная программа, совместимая с протоколом обмена ASCII. Набор из 21 команды очень универсален и предоставляет широкие возможности по управлению процессом передачи данных. Наиболее распространенные из них приведены в табл.4.

Символы в таблице ASCII расположены не случайным образом, а имеют строгий порядок. Кода символов ‘0’…‘9’ получаются добавлением смещения 0x30 к своему числовому представлению. Буквы ‘A’…‘Z’ имеют порядок следования аналогичный латинскому алфавиту и получаются добавлением смещения 0x41 к порядковому номеру буквы в алфавите. То же самое относится к набору из 26 символов нижнего регистра ‘a’…‘z’ для получения, которых необходимо смещение 0x61.

Табл.3. Таблица символов в кодировке ASCII:

Табл.4. Описание наиболее распространенных управляющих символов ASCII: