Деление

Из всех арифметических операций деление занимает особое место. По отношению к умножению деление является обратной операцией и не имеет конечной формулы для определения частного. Деление – единственная арифметическая операция ограниченной точности! Не смотря на это алгоритмы деления достаточно просты. Ниже будут показаны два таких алгоритма, которые используют только операции вычитания и сдвигов. Для того чтобы получить результат в виде целочисленных частного и остатка нужно предварительно убедиться в том, чтобы делимое было больше делителя и, конечно, исключить возникновение запрещённой операции деления на 0. При делении n-разрядного делимого на m-разрядный делитель под частное необходимо отвести n, а под остаток m разрядов.

Частным случаем является деление на целую степень 2:

X/2 = (x_-1*2^n-1 + x_n-2*2^n-2 + … + x₁*2¹ + x₀*2⁰ )/2 = x_n-1*2^n-1 + x_n-2*2^n-2 + … + x₁*2⁰ + x₀*1/2¹

Все коэффициенты x_n двоичного числа X переместились на один разряд вправо (x₀ стал при 1/2¹, x₁ стал при 2⁰ и т.д.). Таким образом для деления двоичного числа на 2ⁿ необходимо произвести сдвиг его содержимого на n разрядов в правую сторону. Так выглядит деление на 2 16-разрядного числа в регистрах R17:R16:

     lsr  R17  ; R17 <- R17 >> 1 (MSB <- 0, флаг С <- LSB)    
     ror  R16  ; R16 <- R16 >> 1 (MSB <- С, флаг С <- LSB)                              

Обратите внимание на то, что после сдвига вправо во флаге переноса С окажется целочисленный остаток (младший коэффициент x0) от деления на 2.

Для другого частного случая деления на 3 существует один очень интересный алгоритм, основанный на разложении дроби X/3 в ряд вида:
   X/3 = X/2 - X/4 + X/8 - X/16 + X/32 - …

Каждый член ряда получается делением X на целую степень 2, что как было показано выше, легко реализуется сдвиговыми операциями. Ниже приведена подпрограмма деления на 3 16-разрядного числа.

; R19:R18 = R17:R16/3
; R19:R18 – частное
; R17:R16 – делимое
; R20 – вспомогательный регистр
 
div16to3:
    clr   R18      ;очищаем вспомогательные регистры R18,R19
    clr   R19      ;при входе в подпрограмму   
du1: rcall shft_right
	brne  PC+2     ;если Z=1, 
    ret            ;то завершаем деление
    add   R18,R16  ;в ином случае добавляем к накопителю
	adc   R19,R17  ;очередной нечётный член ряда
	rcall shift_right
	brne  PC+2     ;если Z=1,
	ret            ;то завершаем деление
    sub   R18,R16  ;в ином случае вычитаем из накопителя
	sbc   R19,R17  ;очередной чётный член ряда
    rjmp  du1

shft_right: 
    lsr   R17      ;производим деление R17:R16 / 2,
	ror   R16      ;получая очередной член ряда
	mov   R20,R17  ;если R20 = R17+R16 = 0 (т.е. R17:R16=0), 
	or    R20,R16  ;то выходим из подпрограммы с флагом Z=1
    ret                             

Этот пример очень эффективен. Его быстродействие ограничено только разрядностью делимого. Более того для делимого произвольной величины обрабатывается оптимальное число членов ряда (до 16), а результат автоматически округляется до ближайшего целого числа.    

Естественно, что в тех случаях, когда необходимо разделить число на 6 можно совместно использовать приемы деления на 2 и 3:
X/6 = (X/2)/3 = (X >> 1)/3 = (X/3) >> 1

Для уменьшения погрешности деление чётных чисел следует начинать с деления на 2 (остаток 0) а, деление нечётных с деления на 3 (алгоритм этого вида деления учитывает остаток).

В общем случае самый естественный и простой способ разделить одно число на другое – это решить уравнение, вытекающее непосредственно из определения операции деления:
X = Z*Y + R,
R < Y, Y ≠ 0,
где X – делимое, Y – делитель, Z – частное, R – целочисленный остаток от деления.

Уравнение содержит два неизвестных параметра Z и R и поэтому не может быть явно разрешено. Для отыскания результата необходимо прибегнуть к итерационному методу: вычитать из делимого делитель до тех пор, пока остаток не окажется меньше делителя. Тогда число циклов вычитания численно даст частное Z, а остаток будет равен целочисленному остатку R от деления. Для примера, произведем следующее деление:
X = 213, Y = 10,
X - Z*Y = R, 213 – 21*10 = 3,
Z = 21, R = 3.    

Мы 21 раз смогли вычесть из 213 по 10 пока не образовался остаток 3<10. Приведённый алгоритм имеет существенный недостаток – скорость его выполнения напрямую зависит от величины частного (числа итераций вычитания), что делает нежелательным его использование для деления больших чисел. Применяется он, в основном, в задачах ограниченных делением однобайтовых величин. Подпрограмма деления:

    ; [R18] + {R17} = R17 / R16 
; R18 – частное 
; R17 – делимое при входе и целочисленный остаток на выходе
; R16 – делитель

div8_8:   
     clr   R18       ;очищаем R18 при входе
     sub   R17,R16   ;производим вычитание R17-R16
     inc   R18         
	 brcc  PC-2      ;до тех пор пока разность R17-R16 > 0
     dec   R18       ;когда разность R17-R16 < 0
     add   R17,R16   ;восстанавливаем R17 и корректируем R18
     ret           

Для чисел большей разрядности необходимо использовать способ деления, основанный на приведенной ниже вычислительной схеме. Для этого представим необходимо выражение операции деления в следующем виде:

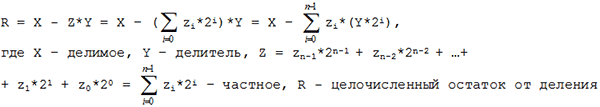
Нахождение частного сводится к отысканию его коэффициентов z_i, которые определяются, согласно формуле, следующим образом: необходимо последовательно сравнивать X с произведениями Y*2ⁱ и если  X > Y*2ⁱ, то в этом случае необходимо произвести вычитание Y*2ⁱ из X, а соответствующий разряд z_i установить в 1; если X < Y*2ⁱ – вычитание пропускается и в этой итерации z_i=0. Эта процедура продолжается до тех пор, пока не останется остаток Ri получаются простым сдвигом Y на i разрядов влево. Аналогично производится деление в любой позиционной системе (метод деления в столбик), но проще всего в двоичной из-за того, что в X может содержаться Y*2ⁱ максимум один раз (на что и указывает единица в соответствующем разряде). Рассмотрим пример деления:

Необходимо обратить внимание на то, что число итераций сравнения должно совпадать с числом значащих разрядов частного (в данном случае n=4 для определения z₀…z₃). Однако разрядность частного заранее никогда не известна и поэтому всегда необходимо знать максимально возможную разрядность результата деления. На практике чаще всего используют вычисления, в которых частное заведомо умещается в 8,16,24 бита (кратно одному байту) и т.д. При этом нужно использовать 8,16,24 итераций сравнения X с Y*2ⁱ, соответственно. С целочисленным остатком R проблем не возникает – его размер ограничен разрядностью Y (R < Y). 

Подпрограмма деления двухбайтового числа на однобайтовое приведена ниже. В ней для сравнения X с Y*2ⁱ (i ∈ {0,…,15}) вместо сдвига делителя Y на n разрядов вправо используется поочерёдный сдвиг делимого на n разрядов влево, а для экономии памяти частное записывается на тоже место, что и делимое. В начале программы осуществляется проверка условия Y ≠ 0, без которого деление не может быть корректно осуществлено.

; [R17:R16] + {R18} = R17:R16 / R20 
; R17:R16 – делимое при входе и частное на выходе
; R20 – делитель
; R18 – целочисленный остаток
; R21, R22 – вспомогательные регистры
; при выходе из подпрограммы в C находится признак ошибки
; если C = 1 – произошла ошибка (R20 = 0)
; если С = 0 – деление успешно выполнено 

div16_8:  
     tst   R20         ;если R20=0 выходим из подпрограммы
     breq  dv3         ;с признаком ошибки C=1
     clr   R18         ;очищаем регистры R18,R19,R21 при  
 	 clr   R19         ;входе в подпрограмму  
     clr   R21
     ldi   R22,16      ;инициализируем счётчик циклов      
dv1: lsl   R16         ;сдвигаем делимое R17:R16 со    
  	 rol   R17         ;вспомогательными регистрами  
     rol   R18         ;R19,R18 на один разряд влево   
	 rol   R19
	 sub   R18,R20     ;осуществляем пробное вычитание 
	 sbc   R19,R21     ;R19:R18 - R20 и если R19:R18 > R20, 
	 ori   R16,0x01    ;то устанавливаем zi=1      
	 brcc  dv2
	 add   R18,R20     ;в ином случае восстанавливаем делимое
	 adc   R19,R21
	 andi  R16,0xFE     ;и устанавливаем zi=0      
dv2: dec   R22         
	 brne  dv1         ;повторяем цикл n=16 раз   
     clc               ;успешно завершаем подпрограмму  
     ret               ;со флагом С=0
dv3: sec               ;выходим из-за ошибки  
     ret               ;с флагом С=1   

Ниже приведена еще одна важная подпрограмма, реализующая  деление 4-хбайтового числа на двухбайтовое с получением 16-разрядных частного и остатка. По своей структуре она аналогична предыдущей, кроме того, что при входе в подпрограмму производится проверка на переполнение результата и тем самым исключаются случаи, при которых частное может не умещаться в отведённых 2-х байтах (например, X = 0x51F356D, Y = 0x100, R = 0x6D, Z = 0x51F35 – имеет разрядность более 16 бит).

; [R17:R16] + {R21:R20} = R19:R18:R17:R16 / R23:R24
; R17:R16 – частное
; R21:R20 - целочисленный остаток
; R19:R18:R17:R16 – делимое 
; R23:R24– делитель
; R25,R26 – вспомогательный регистр
; при выходе из подпрограммы в C находится признак ошибки
; если C = 1 – произошла ошибка (R23:R24 = 0 или размер
; частного больше 2 байт)
; если С = 0 – деление успешно выполнено 

div32_16:  
     mov   R20,R23    ;если R20 = R23 + R24 = 0
 	 or    R20,R24	  ;(т.е. R24:R23 = 0), то выходим из
     breq  dv3        ;подпрограммы с признаком ошибки C=1
     cp    R18,R23    ;если R19:R18 < R24:R23
     cpc   R19,R24    ;(т.е.частное больше 2-х байт), то выходим 
	 brcc  dv3        ;из подпрограммы с признаком ошибки C=1
	 clr   R20        ;очищаем регистры R20,R21,R22,R25 
	 clr   R21        ;при входе в подпрограмму  
	 clr   R22
	 clr   R25
     ldi   R26,32     ;инициализируем счётчик циклов           
dv1: lsl   R16        ;сдвигаем делимое R19:R18:R17:R16 со
	 rol   R17        ;вспомогательными регистрами R20, R21, R22
     rol   R18        ;на один разряд влево
     rol   R19
     rol   R20
	 rol   R21
	 rol   R22
	 sub   R20,R23    ;осуществляем пробное вычитание 
	 sbc   R21,R24    ;R22:R21:R20 - R24:R23 и если
	 sbc   R22,R25    ;R22:R21:R20 > R24:R23,         
     ori   R16,0x01   ;то устанавливаем zi=1      
	 brcc  dv2           
	 add   R20,R23    ;в ином случае восстанавливаем делимое
	 adc   R21,R24
	 adc   R22,R25
	 andi  R16,0xFE   ;и устанавливаем zi=0      
dv2: dec   R26        ;повторяем n=32 раза цикл
	 brne  dv1        ;сравнения R20:R19:R18 с R22:R21 
     clc              ;успешно завершаем подпрограмму
     ret              ;с флагом С=0
dv3: sec              ;выходим из-за ошибки
     ret              

Перейти к следующей части: Формы представления частного в операциях деления

Теги:

• AVR
• Микроконтроллер