или что делать, когда нужны схемы дешевле китайских?
В статье рассмотрен простой высокодобротный узкополосный режекторный фильтр на транзисторах, который отлично работает в частотной полосе до 1 МГц и вполне удовлетворительно до 10 МГц. Выведены простые расчетные формулы для синтеза фильтра при использовании в качестве исходных величин частоты режекции и полосы пропускания. Для расчётов использован математический САПР Maple c пакетом расширений MathSpice [2] и электронный САПР OrCAD [3].
Аналитические задачи в ручную решаются тяжело. Применение MSpice здесь хороший помошник, резко сдвигающий границу сложности решаемых задач. Он делает доступными для радиолюбителей те задачи, которые ранее считались академическими. Пакет расширений Maple под названием MаthSpice (MSpice) [2] предназначен для аналитического решения электронных цепей и функциональных схем, но может быть использован как инструмент создания Spice-моделей сигналов и электронных приборов для различных симуляторов. Подробнее о MSpice можно узнать прочитав стью “MathSpice – аналитический движок для OrCAD и MicroCAP”, Журнал СОВРЕМЕННАЯ ЭЛЕКТРОНИКА, СТА-ПРЕСС, №5, №6, №7, №9, №10, №11, №12 2009 год.
В некоторых устройствах, в которых мы привыкли видеть ОУ, вполне можно обойтись транзисторами. Преимущества использования ОУ для усиления сигналов постоянного тока неоспоримы. Но на переменном токе преимущества ОУ не так серьёзны, как у одиночного транзистора. ОУ с частотой единичного усиления более 10 мГц стоит дорого, в то время, как транзистор с частотой единичного усиления до (100...1000) МГц стоит копейки.
Аналитические расчеты транзисторных устройств несколько сложнее из-за более сложной схемы замещения идеализированного транзистора, по сравнению с идеализированным ОУ. Однако в настоящее время эту проблему облегчает доступность компьютерных вычислений [1], [2].
Очевидно, что транзистор имеет гораздо меньшее число нулей и полюсов, и предельно большое произведение усиления на полосу. Современные транзисторы имеют большой коэффициент усиления по постоянному току h21= 300..1000. Во многих случаях этого достаточно.
В качестве узкополосных режекторных фильтров используются резисторно-конденсаторные двойные Т-образные мостовые фильтры (рис. 1). Их основное преимущество заключается в возможности глубокого подавления отдельных частотных компонентов.
В частотной области, много ниже частоты единичного усиления большинством паразитных параметров транзисторов можно пренебрегать. По этому для расчетов использовалась простейшая схема замещения транзистора, показанная на рис. 2. Она построена на базе источника тока (I1) управляемого напряжением. Её удобно использовать при расчете цепей методом узловых потенциалов.
Рис. 1. Схема узкополосного режекторного фильтра на частоту 6,5 МГц![[Maple Metafile]](/comp/Filer/Filer1.gif)
Составим уравнения Кирхгофа для схемы фильтра и решим её.
| > | restart: with(MSpice): Devices:=[Oдинаковые,[BJT,DC1,2]]: ESolve(Q,`BJT-PSpiceFiles/SCHEMATIC1/SCHEMATIC1.net`): |
![[Maple Plot]](/comp/Filer/Filer2.gif)
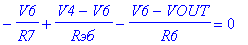
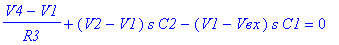
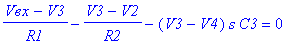
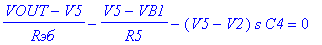
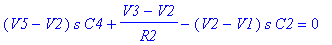
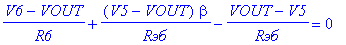
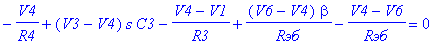
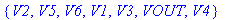
MSpice v8.43: http://pspicelib.narod.ru
Заданы узлы: {VINP, V12V} Источники: [Vвх, VB1, Jэ]
Решения V_NET: [V2, V5, V6, V1, V3, VOUT, V4]
J_NET: [Je, JVвх, JRэб, JVB1, JR5, JC4, JR4, JR1, JC1, JR6, JR2, JR7, JR3, JC2, JC3, JFт, JJэ, Jk, JT]
Найдем передаточную функцию фильтра. Для упрощения формул учтём, что для фильтра с мостом Вина должны выполняться следующие соотношения:
| > | C1:=C: C2:=C: C3:=2*C: R1:=R: R2:=R: R3:=R/2: VB1:=0: # при линейных моделях ПП H:=simplify(VOUT/Vвх); |
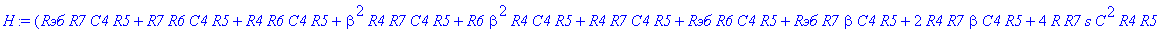
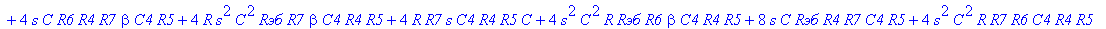
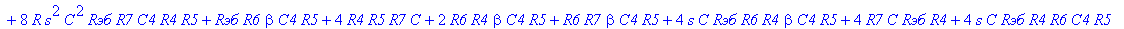
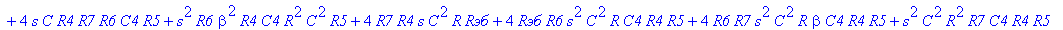
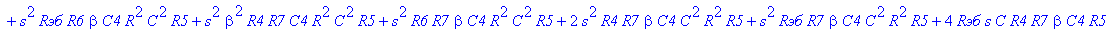
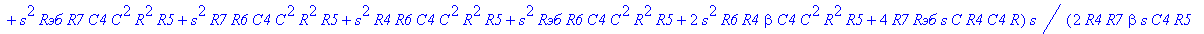
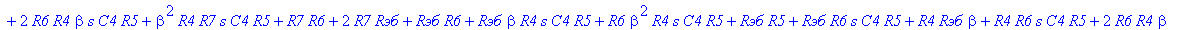
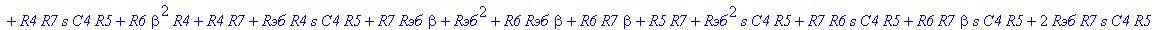
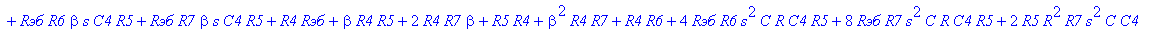
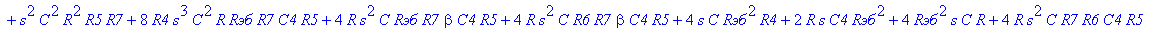
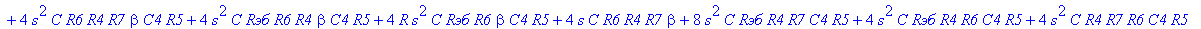
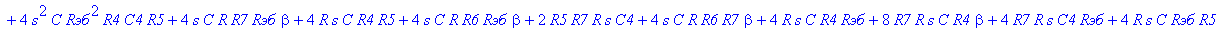
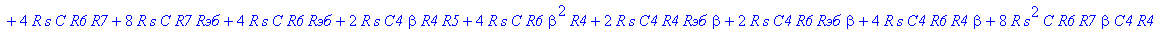
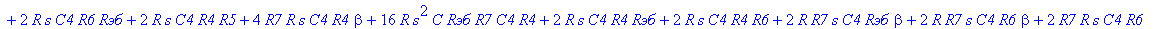
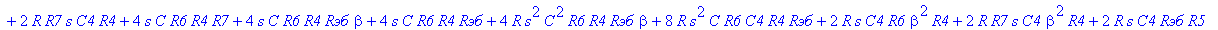
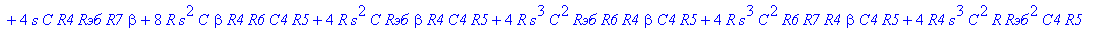
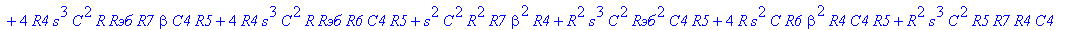
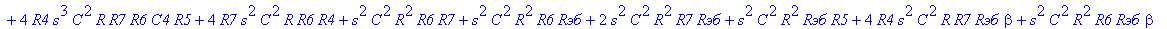
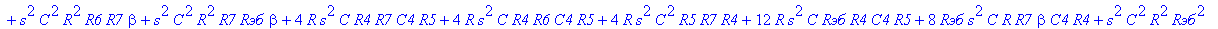
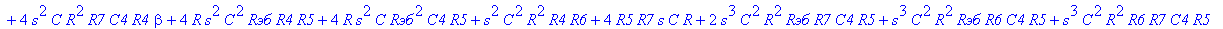
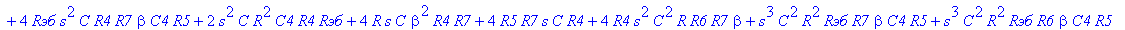
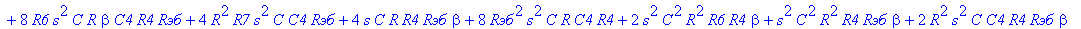
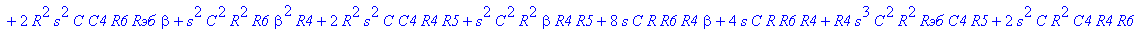
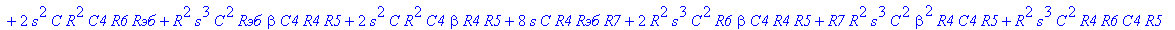
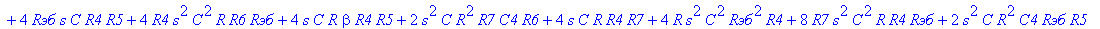
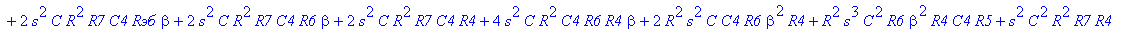
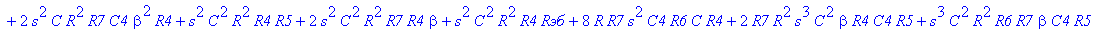
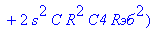
С такой формулой работать трудно!!! Тогда предположим, что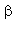 
= oo, C4=oo , R5=oo . Конечно, считать, что транзистор имеет бесконечной усиление, несколько грубовато, но для схемы эмитерного повторителя вполне уместно. Это позволяет получить простые формулы для предварительного расчета. Точные формулы с помощью Maple получить можно, но они будут очень сложными для оценки параметров фильтра (формулы займут несколько страниц). При настройке параметры схемы (добротность) легко скорректировать подбором резистора R6. Выполнив предельный переход, получим более простое выражение для операторного коэффициента передачи (1), более пригодного для анализа.
| > | beta:=x: C4:=x: R5:=x: H:=collect(limit(H,x=infinity),s): 'H'=%, ` (1)`; |
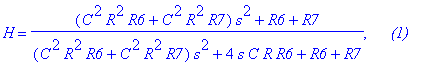
Теперь найдём коэффициент передачи в частотной области, K=K(f), выполнив подстановку s=I*2*Pi*f .
Здесь I - мнимая единица, f - частота [Гц].
| > | K:=simplify(subs(s=I*2*Pi*f,H)): 'K(f)'=%, ` (2)`; |
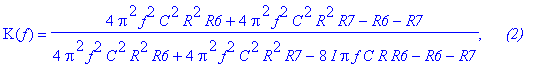
Найдём частоту режекции (3).
| > | Fp=I*solve(diff(K,f)=0,f)[2]: print(%,` (3)`); |
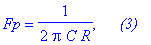
Частоту режекции удобно подстраивать выбором резистора R=R1=R2=2*R3.
| > | R:=solve(%,R): print('R'=R,` (4)`); |
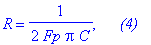
Полоса режекции по уровню 3 дБ
| > | F_3dB:=solve(evalc(abs(K))=subs(f=0,K)/sqrt(2),f): П:=simplify(F_3dB[4]-F_3dB[2]): print('П'=П,` (5)`); |
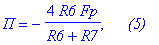
Добротность определяется как Q=Fp/П, отсюда
| > | Q:=Fp/П: 'Q'=Q,` (6)`; |
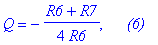
Выразим передаточную функцию через характерестические параметры фильтра, выполнив подстановки R7=4*Qp*R6-R6, C=1/(2*Pi*R*Fp).
Получается очень удобная формула (7), позволяющая получить требуемую режекторную передаточную функцию по Лапласу, ни чего не зная об устройстве фильтра. Здесь Hp(s) - режекторная операторная передаточная функция, Fp - частота режекции, Qp - добротность режектора.
| > | Hp:=simplify(subs(R7=4*Qp*R6-R6,C=1/(2*Pi*R*Fp),H)): 'Hp(s)'=Hp; |
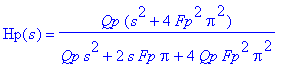
Теперь найдём модуль режекторной функции в частотной области (8).
| > | abs(Kp(f)) = simplify(expand(AVM(Hp,f)),'symbolic'), ` (8)`: |
| > | abs(Kp(f)) = Qp*(f^2-Fp^2)/collect(Qp^2*f^4-2*Qp^2*f^2*Fp^2+Qp^2*Fp^4+Fp^2*f^2,f)^(1/2), ` (8)`: abs(Kp(f)) = Qp*(f^2-Fp^2)/(Qp^2*f^4+collect(-2*Qp^2*Fp^2+Fp^2,Fp)*f^2+Qp^2*Fp^4)^(1/2), ` (8)`; Kp:=Qp*(f^2-Fp^2)/collect(Qp^2*f^4-2*Qp^2*f^2*Fp^2+Qp^2*Fp^4+Fp^2*f^2,f)^(1/2): |
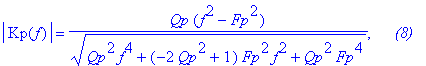
Мы получили очень удобную формулу (8) для синтеза режекторной передаточной функции через характеристические параметры фильтра. Уё можно использовать для цифровых прототипов, при программировании фильтров на микроконтроллерах.
Пример расчёта.
Пусть нам требуется фильтр, обеспечивающий режекцию спектра звукового сигнала телевизионного вещания с центральной частотой Fp=6,5 МГц в полосе П=1МГц. Выберем С=51 пФ и, последовательно пользуясь формулами (4) и (6), рассчитаем остальные компоненты.
| > | Fp:=6.5e6: П:=1e6: C := 51e-12; |
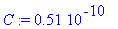
| > | Digits:=5: Q:='Fp/П'=Fp/П; Q:=Fp/П: |
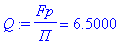
| > | R:='1/(2*Pi*Fp*C)'=evalf(1/(2*Pi*Fp*C)); R:=rhs(%): |
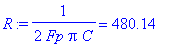
Известно, что усилительные свойства транзистора зависят от тока эмиттера.
В схеме эмиттерного повторителя величина эмиттерного резистора 1 кОм, обеспечит рабочий ток транзистора 6 мА при напряжении питания 12В, что достаточно для сохранения высокого усиления транзистора на высоких частотах.
Выберем R6+R7=1 кОм, тогда R6=(R6+R7)/4/Q=1K/4/Q, а R7=1K-R6.
| > | R6:=1000.0/Q/4: print('R6'=R6); R7:=1000-R6: print('R7'=R7); |
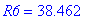
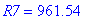
Построим график АЧХ модуля частотного коэффициента передачи нашего режекторного фильтра.
Для этого воспользуемся выражением (8) для модуля передаточной функции, подставив в него рассчитанные величины номиналов компонентов. Эти же величины, округлённые до целого, указаны на схеме фильтра (рис. 1).
| > | Values(AC,PRN,[]);Digits:=5: |
| > | Qp:= '1/4/R6*(R6+R7)'=evalf(1/4/R6*(R6+R7)); Qp:=rhs(%): П:='4*R6*Fp/(R7+R6)'=evalf(4*R6*Fp/(R7+R6))*Unit([Hz]); П:=evalf(4*R6*Fp/(R7+R6)): Fp:= '1/(2*Pi*C*R)'=evalf(1/(2*Pi*C*R))*Unit([Hz]); Fp:=evalf(1/(2*Pi*C*R)): K:=simplify(expand(AVM(H,f))): print('abs(Kp(f))'=Kp); Digits:=10: HSF([H],f=1e6..10e6,"3) semi[abs(Kp(f))]$500 режекторного фильтра |Kp(f)| "); |
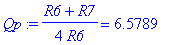
![`П` := 4*R6*Fp/(R6 R7) = .98800e6*Unit([Hz])](/comp/Filer/Filer59.gif)
![Fp := 1/(2*Pi*C*R) = .64996e7*Unit([Hz])](/comp/Filer/Filer60.gif)
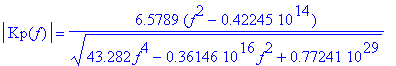
![[Maple Plot]](/comp/Filer/Filer62.gif)
Литература:
1. Петраков О. М. . Аналитические расчёты в электронике. Журнал СХЕМОТЕХНИКА №7, 2006г.
2. Петраков О. М. Цикл статей “MathSpice – аналитический движок для OrCAD и MicroCAP”,
Журнал СОВРЕМЕННАЯ ЭЛЕКТРОНИКА, СТА-ПРЕСС, №5, №6, №7, №9, №10 2009 год. .
3. Разевиг В. Д. Система проектирования OrCAD 9.2. СОЛОН. Москва 2001г.
4. Ефимов И. П. Проектирование электронных фильтров: Методические указания по курсовому проектированию для студентов, обучающихся по направлению 5515.
Составитель И. П. Ефимов. Ульяновск 1999 стр. 32, пример-16.
5. Мошиц Г., Хорн П. Проектирование активных фильтров: Пер. с англ. Мир, 1984.- 320 с, ил.
6. Волович Г. И. Аналоговые и цифровые устройства. 2005г.
7. http://pspicelib.narod.ru Электронный САПР..
8. http://pspice.narod.ru Автоматизация аналитических расчётов.
Автор: Олег Петраков. pspicelib@narod.ru
- BJT Filter 6_5MHz.rar (102 Кб)
Петраков О.
Опубликована: 2009 г.
Вознаградить
Комментарии (0)
|
Я собрал (0) |
Подписаться
Для добавления Вашей сборки необходима регистрация